Painotettu keskiarvo Laskin (Excel-malli)

Painotettu keskimääräinen kaava (sisällysluettelo)

Painotettu keskiarvo
Painotettu keskimääräinen laskin
Painotettu keskimääräinen kaava Excelissä (Excel-mallilla)

Painotettu keskiarvo

Kaava painotetun keskiarvon laskemiseksi on seuraava:

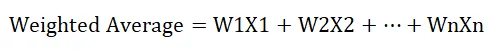
Missä,

W tarkoittaa suhteellista painoa (%)
X tarkoittaa arvoa

Esimerkkejä painotetusta keskimääräisestä kaavasta

Katsotaanpa muutamia esimerkkejä painotetun keskimääräisen kaavan ymmärtämiseksi:

Esimerkki 1

Oletetaan, että Anand on sijoittanut rahat seuraaviin suhteellisiin osuuksiin: 40% sijoitukseen A, 20% sijoitukseen B ja 40% sijoitukseen C. Näiden sijoitusten tuottoprosentti on seuraava: Sijoitus A on 15%, sijoitus B on 10 % ja sijoitus C 20%. Meidän on laskettava painotettu keskiarvo tuottoprosentteille, joita Anand saisi.

Tässä,

Sijoitusten A, B & C suhteelliset painot ovat 40%, 20% ja 40%.
Ja sijoitusten A, B & C arvo (tuottoprosentti) 15%, 10% ja 20%.

Käyttämällä painotettua keskiarvokaavaa saamme-

Painotettu keskiarvo = W1 X1 + W2 X2 + …… + Wn Xn
Painotettu keskiarvo = 40% * 15% + 20% * 10% + 40% * 20%
Painotettu keskiarvo = 16%

Tämä osoittaa, että Anand saa keskimäärin 16%: n painoarvon sijoituksilta A, B & C.

Esimerkki 2

Oletetaan, että Anand on ilmoittautunut matematiikan kurssille, hänen lopullinen arvosana määritetään seuraavien luokkien perusteella: testit 30%, loppukoe 40%, tietokilpailut 15% ja kotitehtävät 15%.

Anand on saanut seuraavan arvosanan jokaisessa luokassa: Testit-80, Loppukoe-65, tietovisat-85, kotitehtävät-90. Nyt meidän on selvitettävä Anandin yleinen arvosana.

Painotetun keskiarvon laskemiseksi prosenttiosuuksilla jokaisen luokan arvo on ensin kerrottava sen prosenttimäärällä. Sitten kaikki nämä uudet arvot on liitettävä yhteen.

Tässä,

Meillä on suhteelliset painot seuraaville luokille:

Testit 30%
Loppukoe 40%
tietokilpailuja 15%
kotitehtävät 15%

Ja arvo (merkit) luokille

Testit-80
Loppukoe-65,
tietokilpailuja-85
kotitehtäviä-90

Käyttämällä painotettua keskiarvokaavaa saamme-

Painotettu keskiarvo = W1 X1 + W2 X2 + …… + WnXn
Painotettu keskiarvo = (30% * 80) + (40% * 65) + (15% * 85) + (15% * 90)
Painotettu keskiarvo = 76, 25 tai 76%

Tämä osoittaa, että Anandin kokonaisluokka on 76%.

Esimerkki 3

Oletetaan, että Jagriti on sijoittanut rahaa eri yritysten osakkeisiin. Jagriti-kanta koostuu 30% osakekannasta A, 15% varastosta B, 30% varastosta C ja loput 25% varastosta D. Odotettu tuotto näiden osakkeiden nykyiseen markkinatilanteeseen nähden on seuraava: A-osakkeen tuotto on 15%, osake B: n tuotto on 12%, osake C: n tuotto on 17% ja D: n tuotto on 16%. Jagriti haluaa laskea keskimääräisen tuotonsa salkusta nykyisen markkinatilanteen mukaan.

Tässä,

Meillä on salkussa olevien osakkeiden suhteelliset painot: A, B, C & D 30%, 15%, 30% ja 25%.
Ja osakkeiden arvo (tuottoprosentti) seuraavasti: A, B, C & D vastaavasti 15%, 12%, 17% ja 16%.

Käyttämällä painotettua keskiarvokaavaa saamme-

Painotettu keskiarvo = W1 X1 + W2 X2 + W3 X3 + W4 X4 …… + Wn Xn
Painotettu keskiarvo = (30% * 15%) + (15% * 12%) + (30% * 17%) + (25% * 16%)
Painotettu keskiarvo = 0, 154 tai 15, 4%

Tämä osoittaa, että Jagriti saa keskimäärin 15, 4% painoarvon tuotot osakekannasta A, B, C ja D.

Selitys painotetusta keskimääräisestä kaavasta

Painotettua keskiarvokaavaa käytetään tietyn lukuarvojen keskiarvon laskemiseen, joilla on erilaiset osuustasot. Painot on esitettävä prosentteina kokonaisvastuullisuudesta. Käytettyjen painojen tulisi olla yhtä suuri kuin 100% tai 1.

Painotetun keskiarvon laskemiseksi tarvitaan suhteellinen paino ja arvo.

Ensimmäinen komponentti on suhteellinen paino ja toinen komponentti on arvotulot. Painotetun keskiarvon laskemiseksi meillä on oltava erityinen punnitus kutakin muuttujaa varten, joka otetaan arvoksi, ja painon on oltava yhtä suuri kuin 100%.

Painotetun keskimääräisen kaavan merkitys ja käyttö

Painotettua keskiarvoa käytetään erilaisissa rahoituskaavoissa. Muutama esimerkki painotetusta keskimääräisestä beeta-arvosta ja painotetusta keskimääräisestä pääomakustannuksesta (WACC).

Olemme perehtyneet ajatukseen löytää sarjan esineiden keskimääräinen keskiarvo tai keskiarvo. Voimme yksinkertaisesti summata kaikkien kohteiden arvot ja jakaa sen kohteiden kokonaismäärällä keskiarvon laskemiseksi. Tämä toimii vain, jos kaikki tuotteet painotetaan tasaisesti. Esimerkiksi laskettaessa kuukauden keskimääräiset matkaviestinlaskut voimme yksinkertaisesti laskea yhteen viimeisen 12 kuukauden laskutetut summat ja jakaa sen kahdellatoista, niin saamme karkean kuvan keskimääräisestä maksetusta laskusta, koska matkapuhelin laskusykli on suunnilleen saman ajanjakson eli yhden kuukauden.

Oletetaan, että haluat laskea matemaattisten oppituntien luokan nykyisen keskimääräisen arvosanan. Yleensä suurin osa luokista antaa eri painoarvoa tentteille kuin kotitehtäville, sisäiselle testille ja kilpailuille. Tässä tapauksessa sinun on laskettava painotettu keskiarvo, joka ottaa kunkin aiheen ominaispainon kurssipisteen laskemiseksi.

Esimerkki muutamasta tapauksesta, joissa jouduttiin käyttämään painotettua keskiarvoa yksinkertaisen keskiarvon sijasta. Ensimmäinen tapaus - Kun haluamme laskea keskiarvon, jolla on erilaiset prosenttiarvot eri luokille. Edellä oleva esimerkki kurssiarvosta on yksi samanlainen tapaus. Ja toiseksi, kun meillä on suuri joukko esineitä, joilla on erilainen säännöllisyys.

Jos yrityksellä on laaja myyntivaihtelu kausituotteen tuotannosta johtuen, se voi käyttää painotetun keskiarvon kaavaa. Ja yritys haluaa laskea muuttuvien kulujen keskiarvon, niin yritys voi käyttää painotetun keskiarvon kaavaa ja ottaa myynnin painona saadakseen paremman käsityksen kustannuksistaan. Ja voi verrata tuottamiensa tai myymiensä määriä.

Painotettu keskimääräinen laskin

Voit käyttää seuraavaa painotetun keskiarvon laskuria

W ₁
X1
W ₂
X2
W ₃
X ₃
W ₄
X ₄
Painotettu keskiarvo

Painotettu keskimääräinen kaava =	W ₁ * X ₁ + W ₂ * X ₂ + W ₃ * X ₃ + W ₄ * X ₄
	0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 =	0

Painotettu keskimääräinen kaava Excelissä (Excel-mallilla)

Tässä tehdään sama esimerkki painotetun keskiarvon kaavasta Excelissä. Se on erittäin helppoa ja yksinkertaista. Sinun on annettava kaksi sisääntuloa, ts. Suhteelliset painot ja tuottoprosentti.

Voit laskea painotetun keskiarvon helposti kaavan avulla mukana olevasta mallista.

sijoitusten A, B & C painotettu keskimääräinen tuotto lasketaan seuraavasti:

Anandin kokonaisluokka lasketaan seuraavasti:

paino Iän keskimääräinen tuotto osakekannasta A, B, C ja D lasketaan seuraavasti:

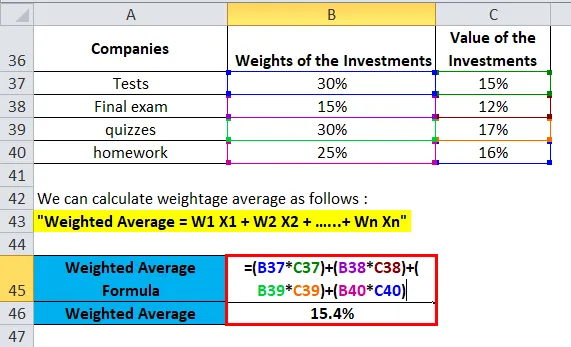
Voit ladata tämän painotetun keskimääräisen Formula Excel -mallin tästä - Painotettu keskimääräinen Formula Excel -malli

Suositellut artikkelit

Tämä on opas painotetun keskiarvon kaavaan. Tässä keskustellaan sen käytöstä käytännön esimerkien kanssa. Tarjoamme sinulle myös painotetun keskiarvon laskurin, jossa on ladattava excel-malli. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -