Excel-regressioanalyysi (sisällysluettelo)
- Regressioanalyysi Excelissä
- Selitys regression matemaattisesta
- Kuinka suorittaa lineaarinen regressio Excelissä?
- # 1 - Regression työkalu, jossa käytetään Analysis ToolPakia Excelissä
- # 2 - Regressioanalyysi käyttämällä Scatterplot-sovellusta Trendline-ohjelmalla Excelissä
Regressioanalyysi Excelissä
Lineaarinen regressio on tilastollinen tekniikka, joka tutkii riippuvan muuttujan ja yhden tai useamman riippumattoman muuttujan välistä lineaarista suhdetta.
- Riippuva muuttuja (eli vaste- / tulosmuuttuja): Onko kiinnostava muuttuja, jonka halusit ennustaa riippumattomien muuttujien käytettävissä olevien tietojen perusteella.
- Riippumaton muuttuja (eli selittävä / ennustava muuttuja): Onko muuttujat / muuttujat, joista vastemuuttuja riippuu. Mikä tarkoittaa, että nämä ovat muuttujia, joiden vastemuuttujaa voidaan ennustaa.
Lineaarisella suhteella tarkoitetaan muutosta riippumattomissa muuttujissa, jotka aiheuttavat muutoksen riippuvaisessa muuttujassa.
Periaatteessa on myös kahden tyyppisiä lineaarisia suhteita.
- Positiivinen lineaarinen suhde: Kun riippumaton muuttuja kasvaa, riippuvainen muuttuja kasvaa myös.
- Negatiivinen lineaarinen suhde: Kun riippumaton muuttuja kasvaa, riippuvainen muuttuja pienenee.
Nämä olivat joitain edellytyksiä, ennen kuin todella siirrytään regressioanalyysiin excelissä.
Lineaarisen regression suorittamiseksi excelissä on kaksi perus tapaa:
- Regressiotyökalu Analysis ToolPakin kautta
- Hajontakaavio trendiviivalla
On oikeastaan vielä yksi menetelmä, joka käyttää manuaalisia kaavoja lineaarisen regression laskemiseen. Mutta miksi sinun pitäisi etsiä sitä, kun excel laskee sinulle?
Siksi aiomme puhua vain kahdesta edellä käsitellystä menetelmästä.
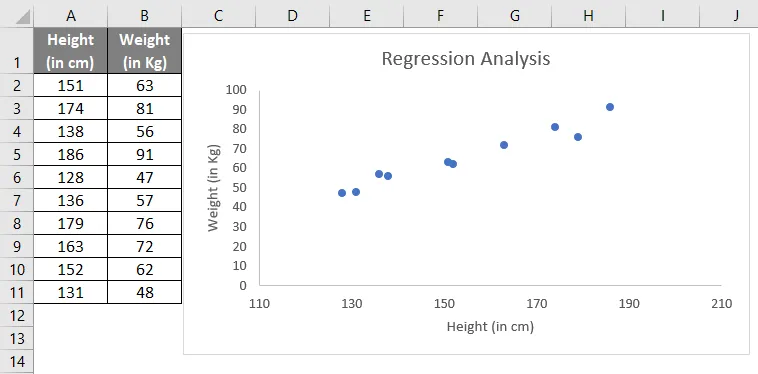
Oletetaan, että sinulla on 10 henkilön pituutta ja painoa koskevia tietoja. Jos piirrät nämä tiedot kaavion kautta, katsotaan mitä se antaa.
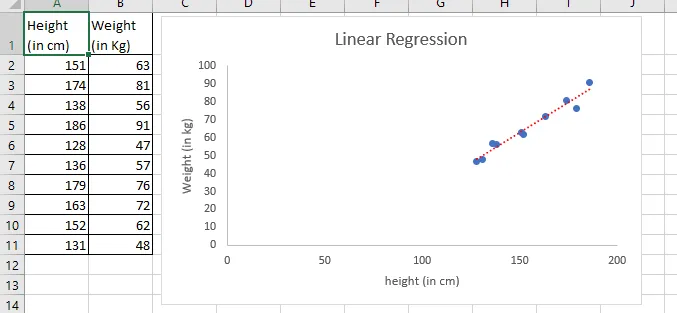
Kuten yllä oleva kuvakaappaus osoittaa, lineaarinen suhde löytyy korkeudesta ja painosta kuvaajan kautta. Älä ota paljon mukaan kuvaajaan, aiomme kuitenkin kaivaa sitä syvälle tämän artikkelin toiseen osaan.
Selitys regression matemaattisesta
Meillä on matemaattinen lauseke lineaariselle regressiolle seuraavasti:
Y = aX + b + ε
Missä,
- Y on riippuvainen muuttuja tai vastemuuttuja.
- X on riippumaton muuttuja tai ennustaja.
- a on regressioviivan kaltevuus. Mikä edustaa sitä, että kun X muuttuu, Y: ssä tapahtuu muutos ”a” -yksiköillä.
- b on sieppaamassa. Se on arvo Y, kun X: n arvo on nolla.
- ε on satunnainen virhetermi. Tapahtuu, koska Y: n ennustettu arvo ei koskaan ole täsmälleen sama kuin annetun X: n todellinen arvo. Tämä virhetermi, meidän ei tarvitse huolehtia. Koska jotkut ohjelmistot tekevät tämän virhetermin laskemisen taustajärjestelmässä. Excel on yksi kyseisistä ohjelmistoista.
Tällöin yhtälöstä tulee,
Y = aX + b
Jotka voidaan esittää seuraavasti:
Paino = a * Korkeus + b
Yritämme selvittää näiden a ja b arvot menetelmillä, joista olemme keskustelleet edellä.
Kuinka suorittaa lineaarinen regressio Excelissä?
Lisäartikkeli selittää Excel: n regressioanalyysin perusteet ja osoittaa muutamia eri tapoja suorittaa lineaarinen regressio Excelissä.
Voit ladata tämän regressioanalyysin Excel-mallin täältä - Regression Analysis Excel Template# 1 - Regression työkalu, jossa käytetään Analysis ToolPakia Excelissä
Esimerkkinämme yritämme sovittaa painoarvojen (joka on riippuvainen muuttuja) regression Korkeus-arvojen (joka on riippumaton muuttuja) avulla.
- Napsauta Excel-laskentataulukossa Tiedot- kohdassa Data-analyysi (läsnä analyysiryhmässä ) .
- Etsi regressio . Valitse se ja paina ok.
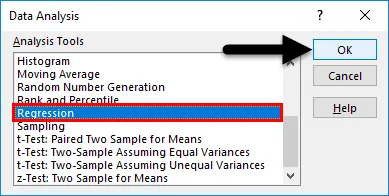
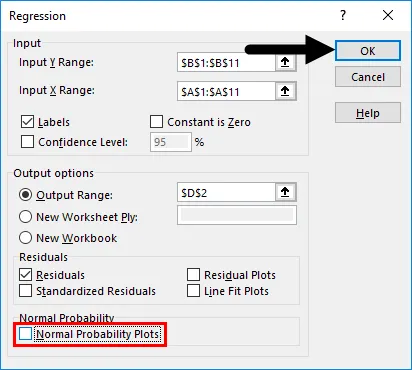
- Käytä seuraavia syötteitä avautuvan Regressio- ruudun alla.
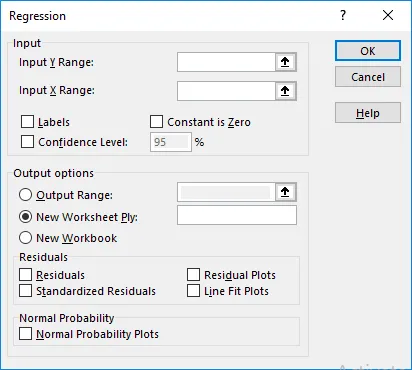
- Input Y-alue : Valitse solut, jotka sisältävät riippuvaisen muuttujan (tässä esimerkissä B1: B11)
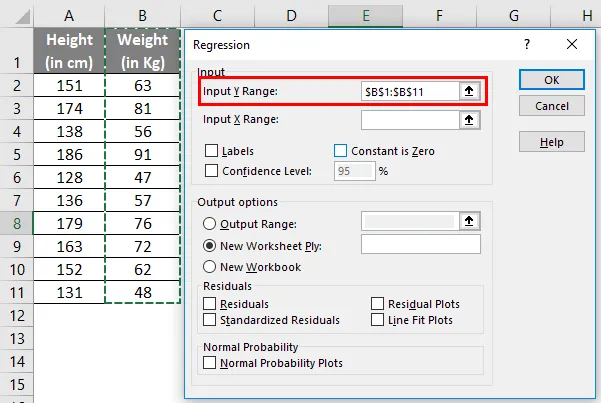
- Input X Range : Valitse solut, jotka sisältävät itsenäisen muuttujan (tässä esimerkissä A1: A11).
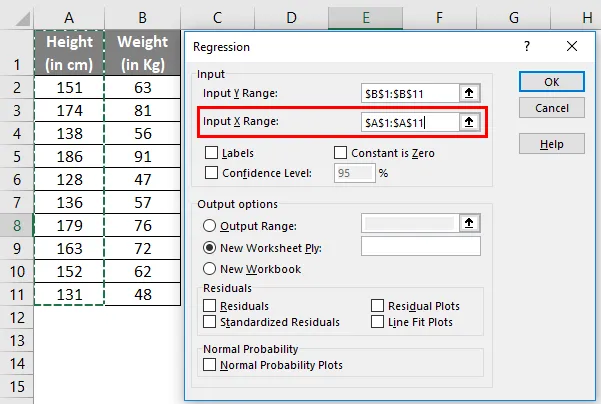
- Valitse Tarrat- ruutu, jos tiedoillasi on sarakkeiden nimet (tässä esimerkissä meillä on sarakkeiden nimet).
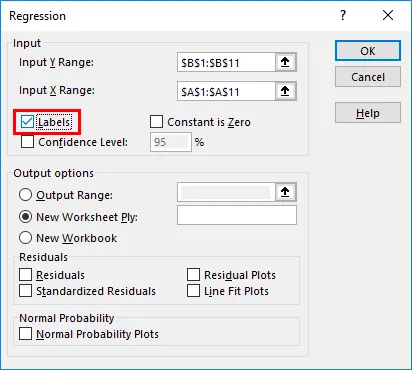
- Luotettavuustaso on oletuksena asetettu 95%: iin, jota voidaan muuttaa käyttäjien vaatimusten mukaan.
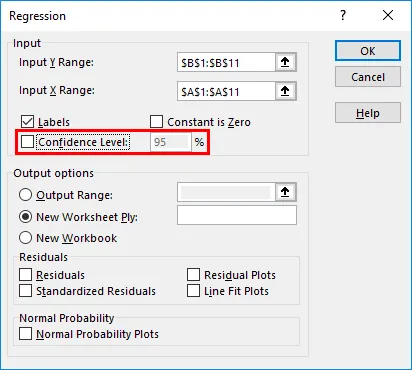
- Tulostusasetukset-kohdassa voit muokata sitä, missä haluat nähdä regressioanalyysin tuotoksen Excelissä. Tässä tapauksessa haluamme nähdä tulosteen samalla arkilla. Siksi annettu alue vastaavasti.
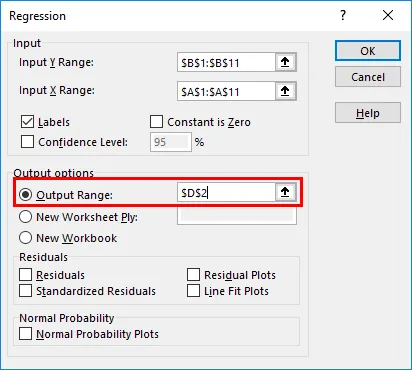
- Jäännösasetukset- vaihtoehdossa sinulla on valinnaisia sisääntuloja, kuten jäännökset, jäännösplotit, standardisoidut jäännökset, linjasovellusplotit, jotka voit valita tarpeen mukaan. Valitse tässä tapauksessa Jäännökset- valintaruutu, jotta näemme jakauman ennustettujen ja todellisten arvojen välillä.
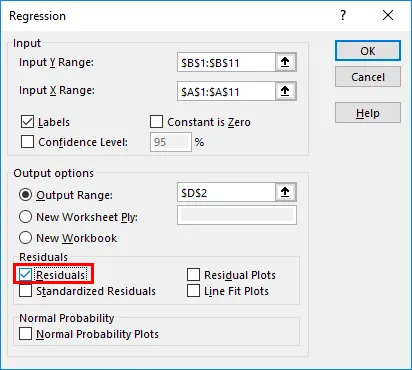
- Kohdassa Normaali todennäköisyys voidaan valita Normaali todennäköisyyskaaviot, joiden avulla voit tarkistaa ennustajien normaliteetin. Napsauta OK .
- Excel laskee regressioanalyysin puolestasi murto-sekunnissa.
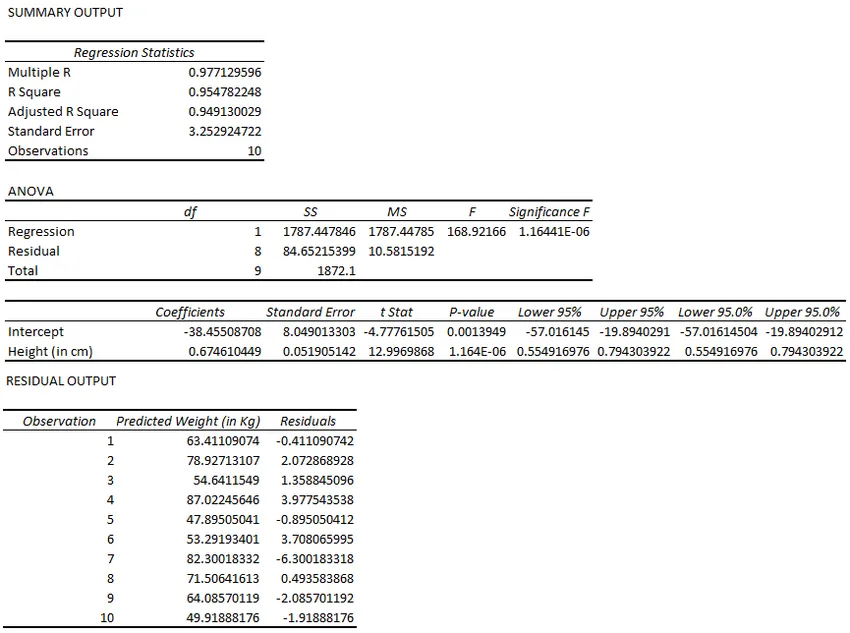
Tähän asti se oli helppoa eikä niin loogista. Tuloksen tulostaminen ja siitä arvokkaiden näkemysten tekeminen on kuitenkin hankala tehtävä.
Yksi tärkeä osa tätä koko lähtöä on R-neliö / Säädetty R-neliö SUMMARY OUTPUT -taulukon alla. Mikä antaa tietoa siitä, kuinka hyvä malli on sopiva. Tässä tapauksessa R-neliön arvo on 0, 9547. Mikä tulkitsee, että mallin tarkkuus on 95, 47% (hyvä istuvuus). Tai jollain muulla kielellä Y-muuttujan tiedot selitetään 95, 47%: lla X-muuttujalla.
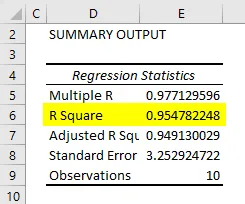
Toinen tärkeä osa koko tulosta on kertoimien taulukko. Se antaa kertoimien arvot, joita voidaan käyttää mallin rakentamiseen tulevia ennusteita varten.

Nyt ennustamisen regressioyhtälöstä tulee:
Paino = 0, 6746 * Korkeus - 38, 45508 ( Korkeuden kaltevuus on 0, 6746… ja sieppauksen arvo on –38, 45508…)
Saitko määritelmäsi? Olet määrittänyt funktion, johon sinun on nyt vain asetettava korkeuden arvo ja saat painon.
# 2 - Regressioanalyysi käyttämällä Scatterplot-sovellusta Trendline-ohjelmalla Excelissä
Nyt näemme, kuinka erinomaisesti voimme sovittaa regressioyhtälön itse sirontapisteeseen.
- Valitse kaksi koko sarakkeesi tietoa (mukaan lukien otsikot).
- Napsauta Lisää ja valitse Scatter Plot kuvaajat-osiosta alla olevan kuvan osoittamalla tavalla.
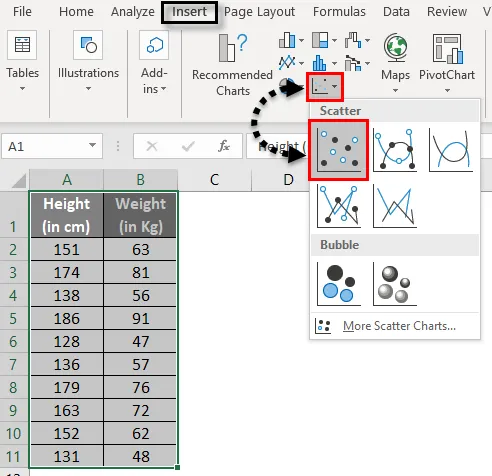
- Katso tuloskaavio.
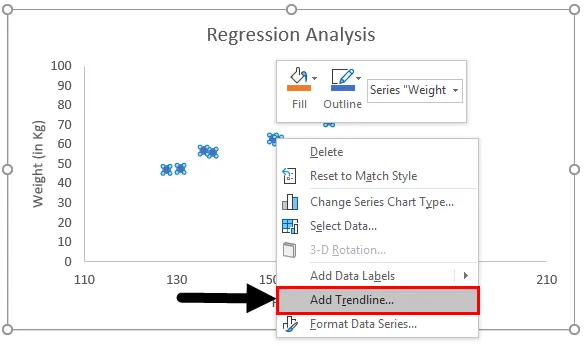
- Nyt meillä on oltava kaaviossa vähiten neliöinen regressioviiva. Lisää tämä rivi napsauttamalla hiiren kakkospainikkeella mitä tahansa kuvaajan datapistettä ja valitsemalla Lisää trendi- vaihtoehto.
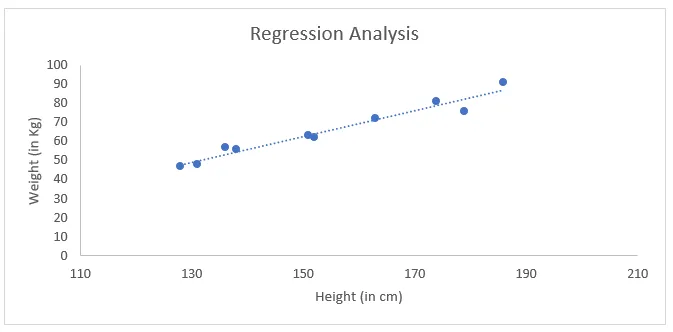
- Se antaa sinulle trendin, jolla on vähiten taantuman neliö, kuten alla.
- Valitse Muotoile suuntaviiva -vaihtoehdon kohtaa Näyttöyhtälö kaaviossa.
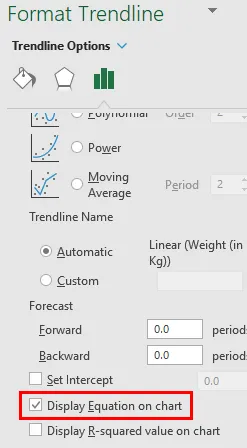
- Sen avulla voit nähdä kaavion pienimmän neliön regressioviivan yhtälön.
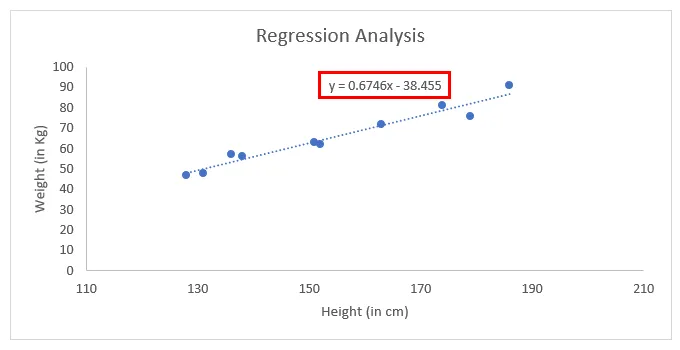
Tämä on yhtälö, jonka avulla voimme ennustaa minkä tahansa korkeusarvojoukon painoarvot.
Muistettavaa regressioanalyysistä Excelissä
- Voit muuttaa trendilinjan asettelua Muotoile trendiviiva -kohdassa hajotuskaaviossa.
- On aina suositeltavaa tarkastella jäljellä olevia kuvaajia, kun teet regressioanalyysiä käyttämällä Data Analysis ToolPak Excel -sovellusta. Se antaa sinulle paremman käsityksen todellisten Y-arvojen ja arvioitujen X-arvojen jakautumisesta.
- Excelin yksinkertainen lineaarinen regressio ei tarvitse ANOVA: ta ja Säädettyä R-neliötä tarkistaakseen. Nämä ominaisuudet voidaan ottaa huomioon monen lineaarisen regression yhteydessä. Mikä ei kuulu tämän artikkelin piiriin.
Suositellut artikkelit
Tämä on opas regressioanalyysiin Excelissä. Tässä keskustellaan siitä, kuinka regressioanalyysi suoritetaan Excelissä yhdessä excel-esimerkkien ja ladattavien Excel-mallien kanssa. Voit myös käydä läpi muiden ehdottamiemme artikkeleidemme -
- Excel-työkalu tietojen analysointiin
- Laske ANOVA Excelissä
- Kuinka löytää Excel-liukuvat keskiarvot
- Z TESTI Esimerkkejä Excelissä