Väestövarianssikaava (sisällysluettelo)
- Väestövarianssikaava
- Esimerkkejä väestön variaatiokaavasta (Excel-mallilla)
Väestövarianssikaava
Tilastoissa varianssi on pohjimmiltaan mittari tietojoukon arvojen hajaantumisen löytämiseksi tietojoukon keskiarvosta. Se mittaa datapisteen etäisyyden ja keskiarvon. Joten korkeampi varianssi, sitä suurempi on dispersio ja datapisteet yleensä kaukana keskiarvosta. Samoin alempi varianssi osoittaa, että datapisteet ovat lähempänä keskiarvoa. Se on erittäin hyödyllinen verrattaessa tietojoukkoja, joilla voi olla sama keskiarvo, mutta eri alue. Väestövarianssi osoittaa samassa mielessä, kuinka väestötietopisteet jakautuvat. Se on etäisyys keskimäärin populaation kustakin datapisteestä keskiarvoon, neliöinä. Lasketaan yleensä väestötietojen varianssi, mutta joskus väestötiedot ovat niin valtavia, ettei varianssin löytämiselle ole taloudellista merkitystä. Siinä tapauksessa lasketaan näytteen varianssi, ja siitä tulee edustava populaation varianssi.
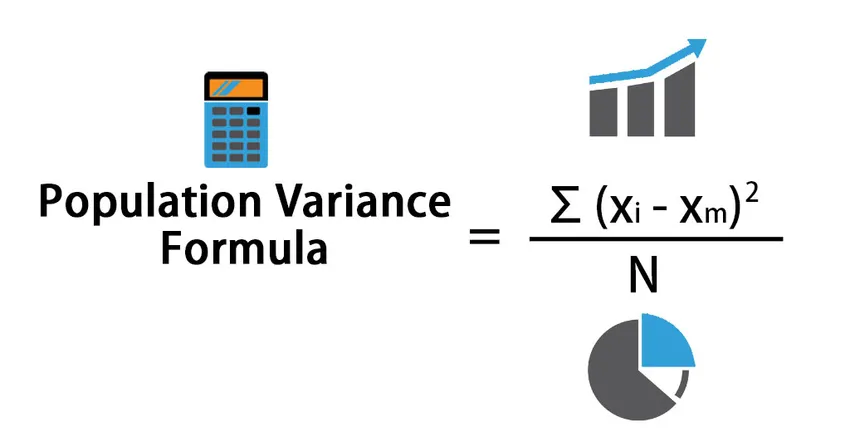
Oletetaan, että sinulla on väestötietojoukko X, jolla on datapisteet (X1, X2 …… ..Xn). Väestysvarianssin kaava annetaan:
Population Variance = Σ (X i – X m ) 2 / N
Missä:
- X i - tietojoukon i - arvo
- X m - tietojoukon keskiarvo
- N - datapisteiden kokonaismäärä
Kaava voi aluksi näyttää hämmentävältä, mutta sen on todella toimittava. Seuraavat vaiheet, joita voidaan seurata laskettaessa väestövarianssia:
- Selvitä, onko työskentelemäsi tietojoukko näytettä vai populaatiota.
- Löydä tietojoukon pisteiden lukumäärä eli n väestölle.
- Seuraava vaihe on löytää keskiarvo. Se on pohjimmiltaan kaikkien arvojen keskiarvo.
- Tämän jälkeen etsi jokaiselle datapisteelle ero keskiarvosta ja neliö sen jälkeen.
- Laske yhteen kaikki arvot yllä olevassa vaiheessa ja jaa ne luvulla 2 laskettu pistemäärä.
On myös toinen tapa laskea varianssi käyttämällä VAR.P () -funktiota populaation varianssille ja VAR.S () -funktiota näytteen varianssille excelissä.
Esimerkkejä väestön variaatiokaavasta (Excel-mallilla)
Otetaan esimerkki ymmärtää paremmin väestövarianssikaavan laskenta.
Voit ladata tämän populaatiovarianssin kaavan Excel-mallin tästä - Väestövarianssin kaava Excel -malliVäestövarianssikaava - esimerkki # 1
Oletetaan, että meillä on kaksi näytedatajoukkoa A & B ja kukin sisältää 20 satunnaista datapistettä. Laske populaation varianssi molemmille tietojoukoille.
Tietojoukko:
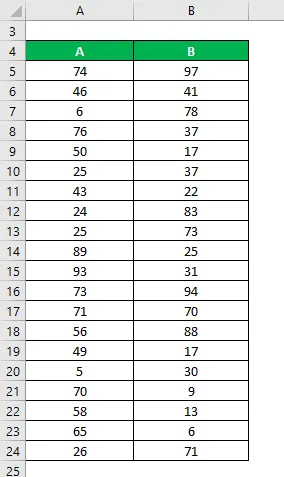
Keskiarvo lasketaan seuraavasti:
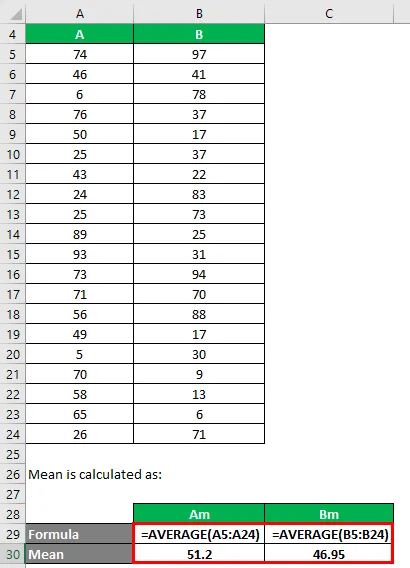
- Tietojoukon A keskiarvo = 51, 2
- Tietojoukon B keskiarvo = 46, 95
Nyt meidän on laskettava ero datapisteiden ja keskiarvon välillä.
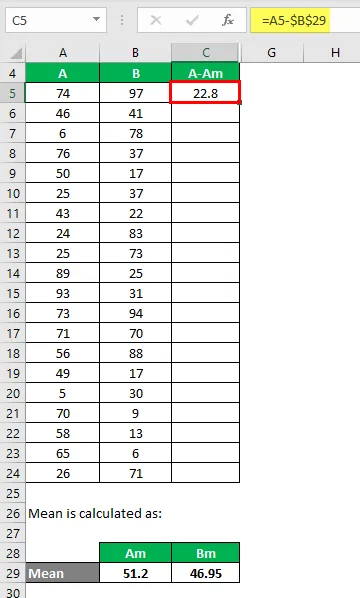
Laske samalla tavalla kaikille A-tietojoukkoille.
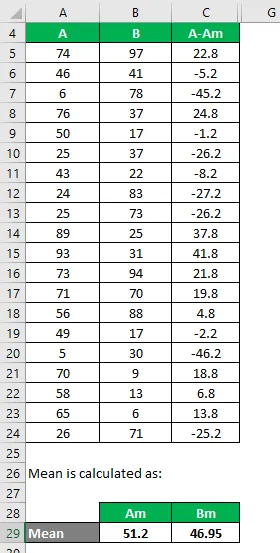
Laske se samalla tavalla myös tietojoukolle B.
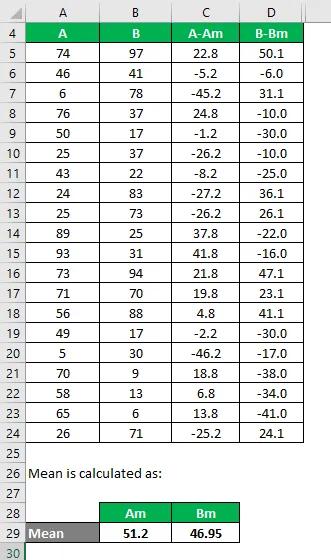
Laske eron neliö molemmille tietojoukoille A ja B.
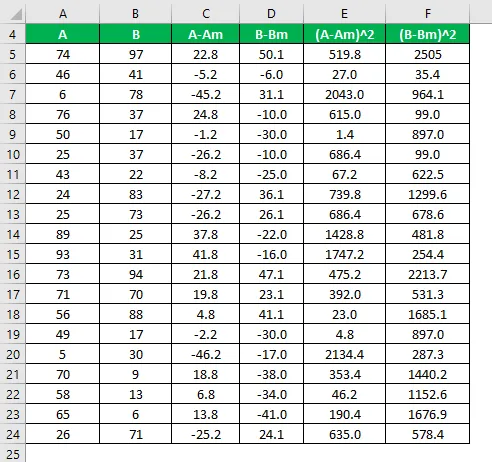
Väestövarianssi lasketaan alla olevan kaavan avulla
Väestövarianssi = Σ (X i - X m ) 2 / N
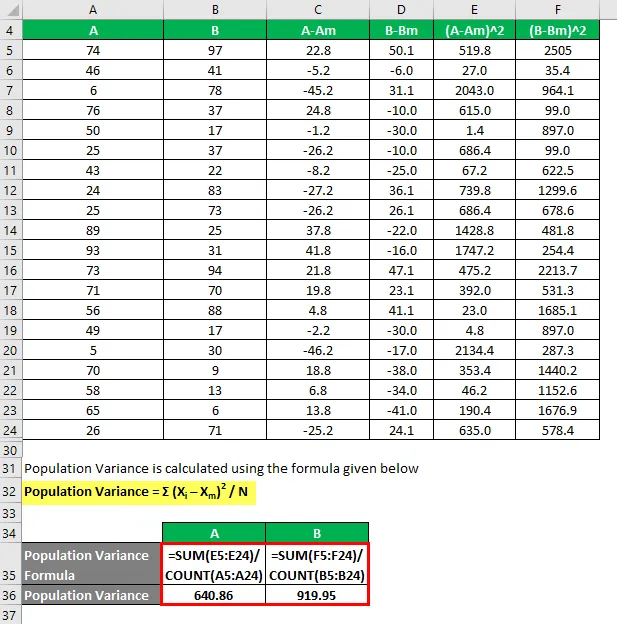
Joten jos näet täällä, B: llä on enemmän varianssia kuin A: lla, mikä tarkoittaa, että B: n datapisteet ovat hajaantuneempia kuin A.
Väestövarianssikaava - esimerkki 2
Sanotaan, että olet erittäin riskitön sijoittaja ja haluat sijoittaa rahaa osakemarkkinoille. Koska riskinottohalusi on alhainen, haluat sijoittaa turvallisiin osakkeisiin, joiden varianssi on alhaisempi.
Haluat analysoida varastot niiden aikaisempien tulosten perusteella, joten olemme päättäneet ottaa 15 vuoden näytteen ja työskennellä näiden tietojen kanssa. Talousneuvojasi on ehdottanut sinulle 4 osaketta, joista voit valita. Haluat valita 2 kantaa näistä 4 joukosta ja päätät sen alhaisemman varianssin perusteella.
Sinulla on tietoa heidän historiallisesta palautumisestaan viimeisen 15 vuoden ajalta.
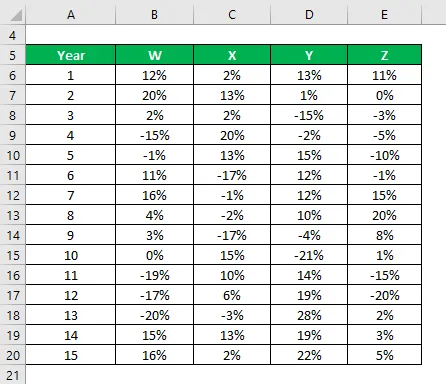
Väestövarianssi lasketaan käyttämällä excel-kaavaa
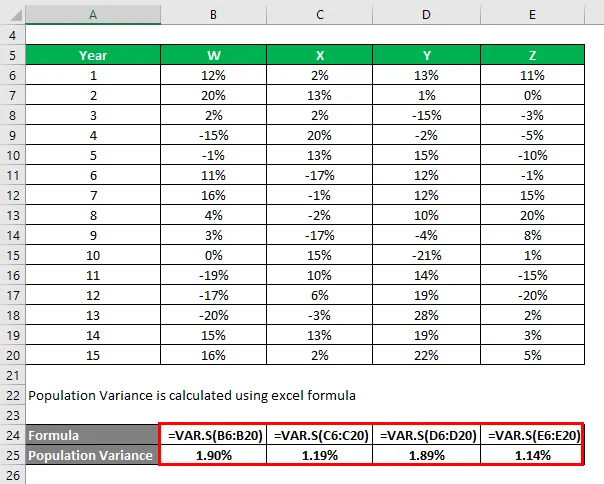
Tietojen perusteella valitset sijoitettavat osakkeet X ja Z, koska niiden varianssi on pienin.
Selitys
Keskustelemme varianssin merkityksestä tilastolliselta kannalta, mutta se auttaa meitä ymmärtämään myös erilaisia taloudellisia suhteita. Varianssi on peruskivi standardipoikkeamalle, joka lasketaan ottamalla varianssin neliöjuuri. Vakiopoikkeama on mittari riskistä, johon sijoitus liittyy, ja kuinka riskialtinen sijoitus on. Sijoittajan riskin perusteella sijoittajat voivat sitten laskea vähimmäistuoton, jota he tarvitsevat korvatakseen kyseisen riskin. Varianssiarvo, koska se on luvun neliö, on aina positiivinen. Tämä voi olla nolla tietojoukolle, jolla on kaikki identtiset kohteet.
Väestövarianssikaavan relevanssi ja käyttö
Varianssi auttaa sijoittajia ja analyytikkoa määrittämään keskihajonnan, joka auttaa edelleen löytämään sijoituksen riski- ja hyötysuhde tai Sharpe-suhde. Periaatteessa kuka tahansa voi ansaita riskittömän tuoton sijoittamalla valtionkassaan ja riskittömiin arvopapereihin. Mutta paluu tämän lisäksi on ylimääräinen tuotto ja sen saavuttamiseksi.
Jotta Sharpe-suhde olisi korkeampi, on parempi sijoitus.
Kuten totesimme, varianssi auttaa löytämään riskipitoisuuden mittaavan standardipoikkeaman, mutta pienempi keskihajonta-arvo ei aina ole suositeltavampi. Jos sijoittajalla on suurempi riskihalu ja hän haluaa sijoittaa aggressiivisemmin, hän on valmis ottamaan enemmän riskejä ja mieluummin suhteellisesti suuremman keskihajonnan kuin riskinhaltija. Joten kaikki riippuu siitä, minkä riskitason sijoittaja on valmis ottamaan.
Suositellut artikkelit
Tämä on opas väestön varianssimalliin. Tässä keskustellaan kuinka lasketaan väestövarianssi sekä käytännön esimerkkejä ja ladattava excel-malli. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- T-jakelukaavan opas
- Esimerkkejä suhteellisesta keskihajontakaavasta
- Kuinka laskea ostovoimapariteetti?
- Kaava salkun varianssille