
F-testikaava (sisällysluettelo)
- Kaava
- esimerkit
Mikä on F-Test Formula?
F-testi on tilastollinen testi, joka auttaa meitä selvittämään, onko kahdella populaatiojoukolla, joiden datapisteiden normaali jakauma on sama standardipoikkeama tai varianssit. Mutta ensisijainen asia F-testin suorittamiseksi on, että tietojoukkojen tulisi olla normaalijakautuneita. Tätä sovelletaan F-jakaumaan nollahypoteesin alla. F-testi on erittäin tärkeä osa varianssianalyysiä (ANOVA) ja se lasketaan ottamalla kahden eri tietojoukon kahden varianssin suhteet. Kuten tiedämme, että varianssit antavat meille tietoja datapisteiden hajaantumisesta. F-testiä käytetään myös erilaisissa testeissä, kuten regressioanalyysissä, Chow-testissä jne.
F-testin kaava:
F-testille ei ole yksinkertaista kaavaa, mutta se on joukko vaiheita, jotka meidän on noudatettava:
Vaihe 1: F-testin suorittamiseksi on ensin määritettävä nollahypoteesi ja vaihtoehtoinen hypoteesi. Ne antavat:
- H0 (nollahypoteesi): Ensimmäisen tietojoukon varianssi = toisen tietojoukon varianssi
- Ha: Ensimmäisen tietojoukon varianssi < Toisen tietojoukon varianssi (alempaan yksisuuntaiseen testiin)
- Ha: Ensimmäisen tietojoukon varianssi> Toisen tietojoukon varianssi (ylempään yksisuuntaiseen testiin)
- Ha: Ensimmäisen tietojoukon varianssi ≠ Toisen tietojoukon varianssi (kaksisuuntaiseen testiin)
Vaihe 2: Seuraava asia, joka meidän on tehtävä, on se, että meidän on selvitettävä merkityksen taso ja määritettävä sitten sekä osoittajan että nimittäjän vapausasteet. Tämä auttaa meitä määrittämään heidän kriittiset arvonsa. Vapausaste on näytteen koko -1.
Vaihe 3: F-testikaava:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Vaihe 4: Etsi F-taulukosta F-kriittinen arvo ottaen huomioon vapausaste ja merkitsevyystaso.
Vaihe 5: Vertaa näitä kahta arvoa ja jos kriittinen arvo on pienempi kuin F-arvo, voit hylätä nollahypoteesin.
Esimerkkejä F-testikaavasta (Excel-mallilla)
Otetaan esimerkki ymmärtää F-testin laskenta paremmin.
Voit ladata tämän F-TEST Formula Excel -mallin täältä - F-TEST Formula Excel TemplateF-testikaava - esimerkki 1
Oletetaan, että meillä on kaksi tietojoukkoa A & B, jotka sisältävät erilaisia datapisteitä. Suorita F-testi selvittääksesi, voimmeko hylätä nollahypoteesin 1%: n merkitsevyystasolla.
Tietojoukot:
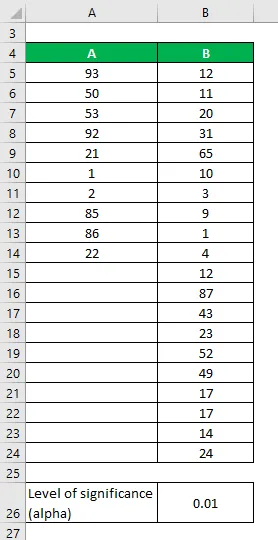
Ratkaisu:
Nollahypoteesi: A: n varianssi = B: n varianssi
Vapausaste lasketaan
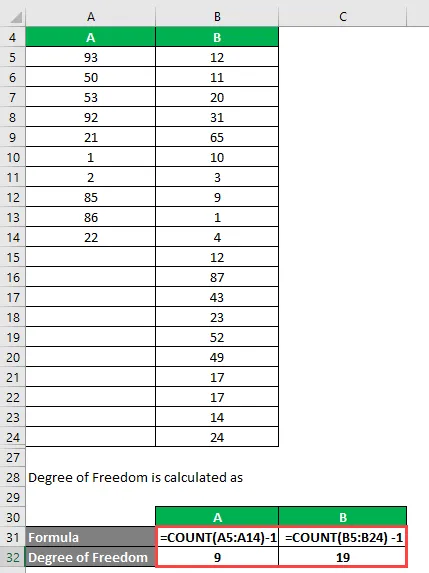
Vapausaste
- A = 10 - 1 = 9: lle
- B: lle = 20 - 1 = 19
Vaihtelu lasketaan:

- Varianssi A = 1385, 61
- B: n varianssi = 521, 22
F Arvo lasketaan alla olevan kaavan avulla
F Arvo = Ensimmäisen tietojoukon varianssi / Toisen tietojoukon varianssi
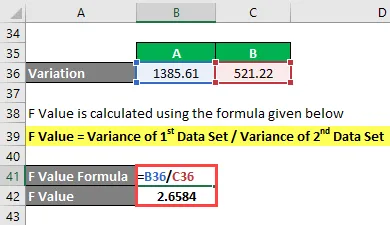
- F-arvo = 1385, 61 / 521, 22
- F-arvo = 2, 6584
F-Taulukko:
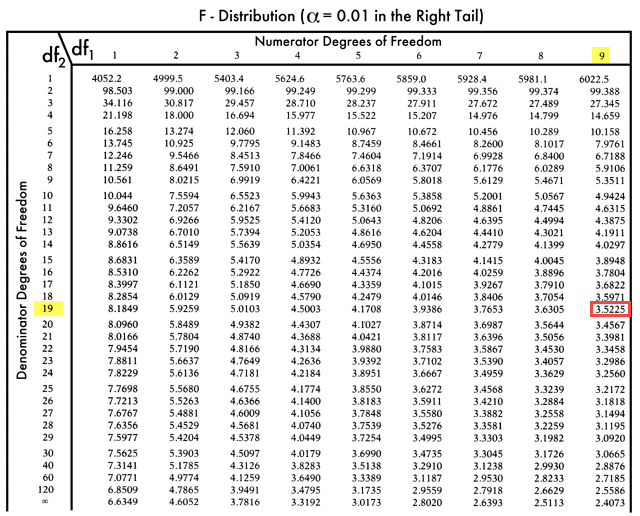
Joten F kriittinen arvo = 3, 5225
Koska F kriittinen on suurempi kuin F-arvo, emme voi hylätä nollahypoteesia.
F-testikaava - esimerkki 2
Oletetaan, että työskentelet tutkimusyrityksessä ja haluatko hiilidioksidipäästöjen tason, joka tapahtuu kahdessa eri tuotemerkin savukkeessa ja ovatko ne huomattavasti erilaisia vai eivät. Analyysissäsi olet kerännyt seuraavat tiedot:
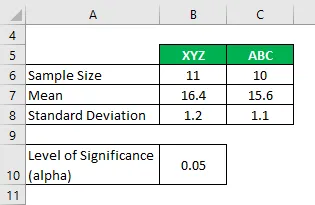
Ratkaisu:
Vapausaste lasketaan
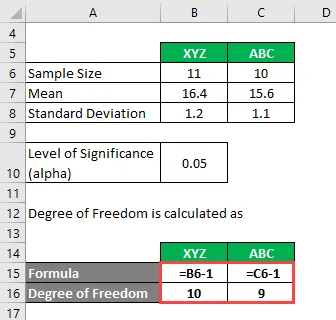
Vapausaste
- XYZ = 11 - 1 = 10: lle
- Jos ABC = 10 - 1 = 9
Vaihtelu lasketaan:
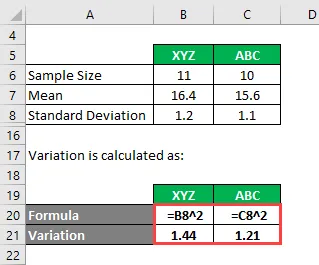
- XYZ: n varianssi = 1, 2 2 = 1, 44
- ABC: n varianssi = 1, 1 2 = 1, 21
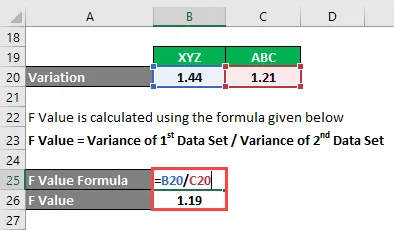
- F-arvo = 1, 44 / 1, 21
- F-arvo = 1, 19
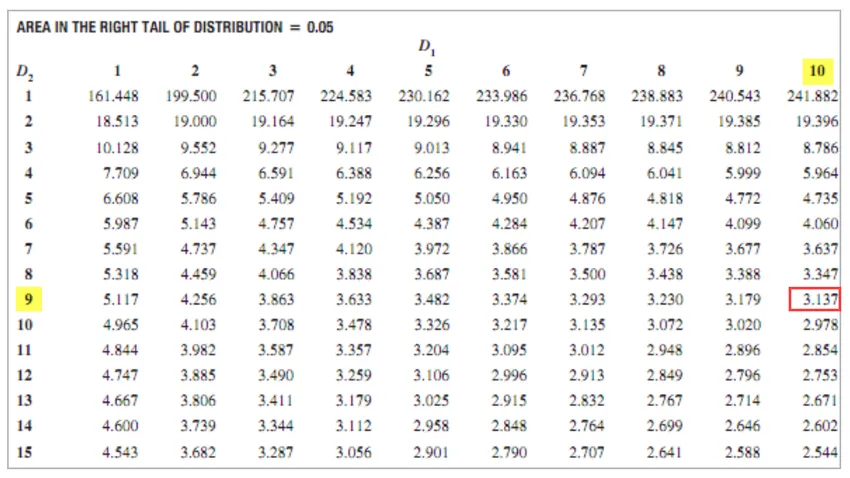
F Kriittinen arvo = 3, 137
Koska F-kriittinen> F-arvo, nollahypoteesiä ei voida hylätä.
Selitys
Yllä olevissa esimerkeissä olemme nähneet F-Testin käytön ja miten se suoritetaan. Mutta on olemassa joukko oletuksia, jotka meidän on oltava varovaisia ennen F-Testin suorittamista, muuten emme saa vaadittuja tuloksia:
- Ensimmäinen asia on, että meidän on aina asetettava korkeampi varianssiarvolaskuri laskettaessa F-arvoa. Joten jos F = V1 / V2, V1: n tulisi olla> V2
- Jos haluamme suorittaa 2 häntätestiä, meidän on jaettava merkitsevyystaso 2: lla ja se on oikea taso kriittisen arvon löytämiseksi
- Käytämme vain varianssia F-arvon laskentaan ja jos meille annetaan vakiopoikkeamat, kuten esimerkissä 2, niiden on oltava neliöinä varianssin löytämiseksi.
- Molempien näytteiden tulee olla toisistaan riippumattomia ja näytteen koon olla alle 30 mm
- Väestöjoukot, joista näytteet otetaan, on jaettava normaalisti
Nämä ovat keskeisiä parametreja / oletuksia, joista tulisi huolehtia suorittaessaan F-testiä.
F-testikaavan relevanssi ja käyttö
F-testi, kuten edellä käsiteltiin, auttaa meitä tarkistamaan kahden populaation variaatioiden tasa-arvon. Joten kun meillä on kaksi riippumatonta näytettä, jotka on otettu normaalista populaatiosta ja haluamme tarkistaa, onko niillä sama variaatio vai ei, käytämme F-testiä. F-testillä on myös suuri merkitys regressioanalyysissä ja myös R2: n merkityksen testaamisessa. Joten pähkinänkuoressa, F-testi on erittäin tärkeä työkalu tilastoissa, jos haluamme verrata kahden tai useamman tietojoukon variaatiota. Mutta kaikki oletukset tulisi pitää mielessä ennen testin suorittamista.
Suositellut artikkelit
Tämä on opas F-Test Formulaan. Tässä keskustellaan kuinka laskea F-testi yhdessä käytännön esimerkkien ja ladattavien excel-mallien kanssa. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- T-jakelukaava
- Joukkovelkakirjojen hinnoittelun kaava
- Prosenttivirhekaava
- NOPAT-kaavan laskeminen