
Johdanto keskihajontaesimerkkeihin
Vakiopoikkeamista on runsaasti esimerkkejä. Vakiopoikkeama on tietojoukon hajonnan mitta eli ts. Kuinka hajaantuneet numerot ovat. On hyödyllistä verrata erilaisia tietojoukkoja, joilla voi olla sama keskiarvo, mutta eri alue. Seuraava erilainen standardipoikkeama antaa ymmärryksen yleisimmistä tilanteista, joissa standardipoikkeama lasketaan ja kuinka voidaan laskea sama
Esimerkkejä keskihajonnasta
Alla on esimerkkejä keskihajonnasta
Vakiopoikkeama - esimerkki 1
Yrityksen Z osake myy 50 dollaria osakkeelta ja tarjoaa seuraavan vuoden voitot seuraavalta vuodelta:
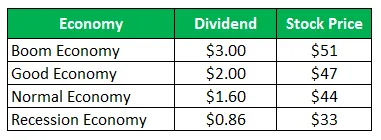
Laske keskihajonta, kun kaikki neljä skenaariota on annettu yhtä todennäköisesti.
Ratkaisu:
Pitoajanjakson tuoton (HPR) laskelmat ovat seuraavat -
HPR: n kaava
HPR = ((kauden lopun arvo - alkuperäinen arvo) + tulo) / alkuperäinen arvo) * 100
Puomitaloudelle
- HPR (puomi) = ((51-50) + 3) / 50 = 8, 00%
- HPR (hyvä) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normaali) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (taantuma) = ((33-50) + 0, 86) / 50 = -32, 28%
Odotetun tuoton laskeminen
Koska kaikki skenaariot ovat yhtä todennäköisiä, niin kaikkien todennäköisyys on ¼
Odotetun palautumisen kaava
Odotettu tuotto = (Puomin todennäköisyys * Paluu puomista) + (Hyvän todennäköisyys * Paluu hyvältä) + (Normaalin todennäköisyys * Paluu normaalista) + (Taantuman todennäköisyys * Paluu taantumasta)
- Odotettu tuotto = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Odotettu tuotto = -8.77%
Keskihajonnan laskeminen
Varianssikaava
Varianssi = (Puomin todennäköisyys * (Paluu puomista - Koko odotettu tuotto) 2) + (Hyvän todennäköisyys * (Paluu hyvältä - Koko odotettu tuotto) 2) + (Normaalin todennäköisyys * (Paluu normaalista - Koko odotettu tuotto) 2 ) + (Taantuman todennäköisyys * (Paluu taantumasta - Koko odotettu tuotto) 2)
- Varianssi = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Varianssi = 219, 95
Standardipoikkeaman kaava
Vakiopoikkeama on varianssin neliöjuuri
Vakiopoikkeama = √Varianssi
- Vakiopoikkeama = √ 219.95
- Vakiopoikkeama = 14.83%
Esimerkki keskihajonnasta - 2
Vakiopoikkeama kahden salkussa olevan yrityksen tapauksessa
Yhtiön A kantaosakkeet myyvät 28 dollaria osakkeelta ja samat tarjoukset seuraavan vuoden voitto-osuuksilla

Yhtiön B kantaosakkeet myyvät 93 dollaria osakkeelta ja tarjoavat seuraavia voittoja seuraavalle vuodelle:

(a) Laske yrityksen A keskihajonta
(b) Laske yrityksen B keskihajonta
(c) Laske salkun keskihajonta, jos puolet sijoituksesta on tehty yritykselle A ja loput puolet yritykselle B
Ratkaisu:
Yritykselle A
Pitoajanjakson tuoton (HPR) laskelmat
HPR: n kaava
HPR = ((kauden lopun arvo - alkuperäinen arvo) + tulo) / alkuperäinen arvo) * 100
- HPR (puomi) = ((20 - 28) + 1) / 28 = -25, 00%
- HPR (normaali) = ((30 - 28) + 1, 50 / 28 = 12, 50%
- HPR (taantuma) = ((38 - 28) + 5) / 28 = 53, 57%
Yrityksen A odotettavissa olevan tuoton laskeminen
Odotetun palautumisen kaava
Odotettu tuotto = (Puomin todennäköisyys * Paluu puomista) + (Normaalin todennäköisyys * Paluu normaalilta) + (Taantuman todennäköisyys * Paluu lamasta)
- Odotettu tuotto = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Odotettu tuotto = 3, 84%
Vakiopoikkeamayrityksen laskeminen
Varianssikaava
Varianssi = (Puomin todennäköisyys * (Paluu puomista - Koko odotettu tuotto) 2) + (Normaalin todennäköisyys * (Paluu normaalista - Koko odotettu tuotto) 2 ) + (Taantuman todennäköisyys * (Paluu lamasta - Odotettu kokonaistuotto) 2)
- Varianssi = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varianssi = 895, 15
Standardipoikkeaman kaava
Vakiopoikkeama on varianssin neliöjuuri
Vakiopoikkeama = √Varianssi
- Vakiopoikkeama = √ 895.15
- Keskihajonta = 29, 92%
Yritykselle B
Pitoajanjakson tuoton (HPR) laskelmat
HPR: n kaava
HPR = ((kauden lopun arvo - alkuperäinen arvo) + tulo) / alkuperäinen arvo) * 100
HPR (puomi) = ((200-93) +7) / 93 = 122, 58%
HPR (normaali) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (taantuma) = ((4-93) +2) / 93 = -93, 55%
Odotetun tuoton laskeminen
Odotetun palautumisen kaava
Odotettu tuotto = (Puomin todennäköisyys * Paluu puomista) + (Normaalin todennäköisyys * Paluu normaalilta) + (Taantuman todennäköisyys * Paluu lamasta)
- Odotettu tuotto = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Odotettu tuotto = 43, 04%
Keskihajonnan laskeminen
Varianssikaava
Varianssi = (Puomin todennäköisyys * (Paluu puomista - Koko odotettu tuotto) 2) + (Normaalin todennäköisyys * (Paluu normaalista - Koko odotettu tuotto) 2 ) + (Taantuman todennäköisyys * (Paluu lamasta - Odotettu kokonaistuotto) 2)
- Varianssi = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Varianssi = 6783, 65
Standardipoikkeaman kaava
Vakiopoikkeama on varianssin neliöjuuri
Vakiopoikkeama = √Varianssi
- Vakiopoikkeama = √6783.65
- Keskihajonta = 82, 36%
Lasketaan odotettavissa oleva tuotto ja keskihajonta sellaiselle salkussa, joka on sijoitettu osaksi yritystä A ja puoli yritystä B.
Yrityksen A keskihajonta = 29, 92%
Yrityksen B keskihajonta = 82, 36%
Yrityksen A paino = 0, 50
Yrityksen B paino = 0, 50
Salkun keskihajonnan kaava
Salkun keskihajonta = (Yrityksen A paino * Yrityksen A odotettu tuotto) + ((Yrityksen B paino * Yrityksen B odotettu tuotto)
- Salkun keskihajonta = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Salkun keskihajonta = 56, 14%
analyysi
Salkun keskihajonta on pienempi kuin kummankin osakekannan yksilöllä, koska osakkeet ovat hajautettu eri osakkeisiin. Hajauttaminen johtaa riskin pienenemiseen, ellei salkusijoitusten tuottojen välillä ole täydellistä korrelaatiota.
Johtopäätös - Esimerkkejä keskihajonnasta
Vakiopoikkeamalla mitataan tietojoukon hajonta suhteessa sen keskiarvoon. Se lasketaan varianssin neliöjuurena. Mitä suurempi on arvopaperin keskihajonta, sitä suurempi on variaatio kunkin hinnan ja keskiarvon välillä, mikä osoittaa, että hintaluokka on suuri. Edellä mainitut esimerkit ovat joitain esimerkkejä keskihajonnasta eri tavoin. On myös monia muita esimerkkejä, jotka osoittavat, että keskihajonta voidaan laskea muilla tiedoilla.
Suositellut artikkelit
Tämä on opas vakiopoikkeamaesimerkkeihin. Tässä keskustellaan monista esimerkkeistä keskihajonnasta yhdessä yksityiskohtaisen selityksen kanssa . Saatat myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Kiinteät kustannukset Esimerkki
- Esimerkki muuttuvasta kustannuslaskelmasta
- Kvantitatiivinen tutkimusesimerkki
- Esimerkkejä monopolistisesta kilpailusta