Mediaani kaava (sisällysluettelo)
- Mediaani kaava
- Median Formula Laskin
- Median kaava Excelissä (Excel-mallilla)
Mediaani kaava
Mediaani on tietojoukon keskiarvo. Annetussa tilastossa ryhmiteltyjen tai ryhmittelemättömien tietojoukkojen n määrässä mediaani on tietojoukon keskeltä löytyvä luku. Sitä käytetään monissa tosielämän tilanteissa.
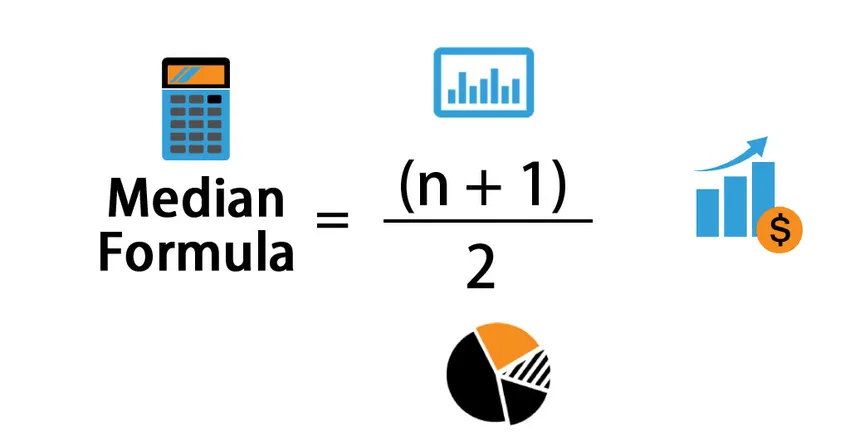
Mediaani lasketaan seuraavan kaavan avulla.
Median = (n + 1) / 2
Jos otat yksinkertaisen esimerkin, 1, 2, 3, 4, 5. Keskiarvo on 3. Voimme löytää sen manuaalisesti, koska tämä on pieni datajoukko. Jos käytät samaa datajoukkoa yllä olevassa kaavassa, n = 5, siis mediaani = (5 + 1) / 2 = 3. Joten kolmas luku on mediaani. Suurelle määrälle dataa mediaanin löytäminen manuaalisesti ei ole mahdollista. Joten on välttämätöntä käyttää kaavaa suurelle joukolle tietojoukkoja.
Esimerkkejä mediaanikaavasta
Otetaan esimerkki ymmärtää mediaani kaavan laskenta paremmin.
Voit ladata tämän Median Excel -mallin täältä - Median Excel TemplateEsimerkki # 1.1 - Pariton määrän lukujen mediaanin löytäminen
Tarkastellaan pientä tietojoukkoa A = 42, 21, 34, 65, 90, 45, 109. Laske käytettävissä olevista tiedoista mediaani.
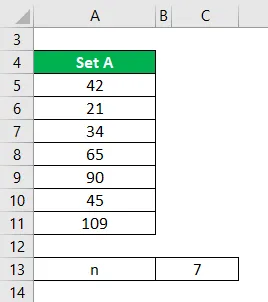
Ratkaisu:
Järjestä tietojoukko nousevaan järjestykseen.
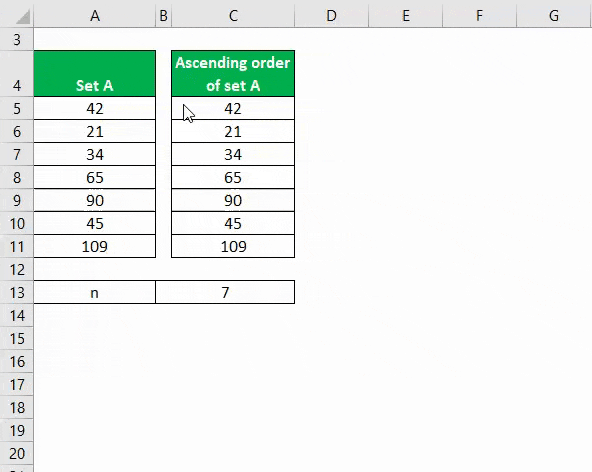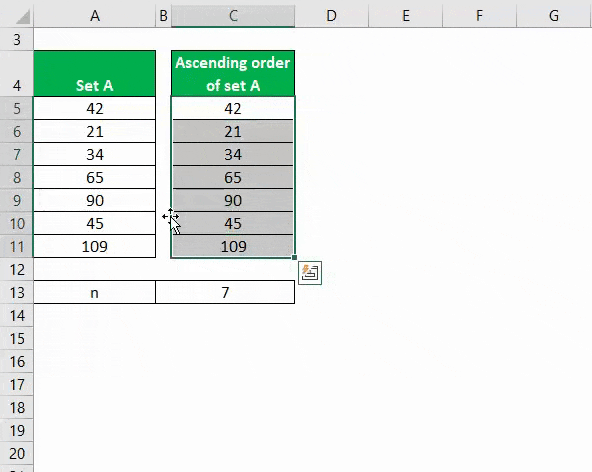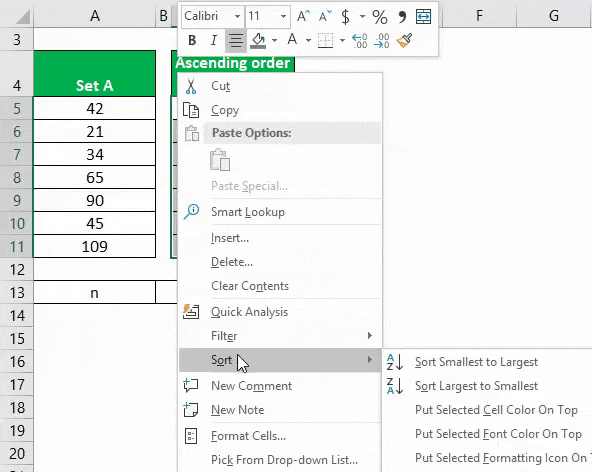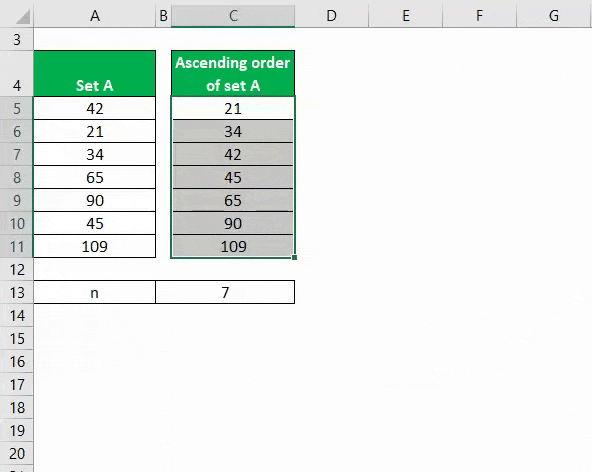
Mediaani lasketaan alla olevan kaavan avulla
Mediaani = (n + 1) / 2
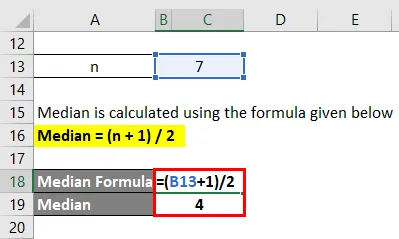
- Mediaani = (7 + 1) / 2
- Mediaani = 8/2
- Mediaani = 4
Tässä 4. arvo on 45. Joten 45 on tämän tietojoukon mediaani.
Esimerkki # 1.2
Tarkastellaan suurta tietojoukkoa B = 1, 2, 3…, 51.
Täällä kokonaismäärät ovat 51. Joten n = 51.
Mediaani lasketaan alla olevan kaavan avulla
Mediaani = (n + 1) / 2
- Mediaani = (51 + 1) / 2
- Mediaani = 52/2
- Mediaani = 26
Joten 26. luku on mediaaniarvo. Joten 25 numeron tulisi olla mediaanin alapuolella, 26. luvun on mediaani ja jälleen 25 numeron on oltava edellä.
Esimerkki # 2.1 - Tasaisen määrän lukujen mediaanin löytäminen
Tarkastellaan pientä tietojoukkoa C = 2, 5, 89, 40, 66, 33, 14, 23, 90, 101. Laske käytettävissä olevien tietojen perusteella mediaani.
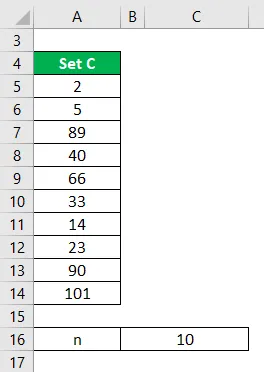
Ratkaisu:
Järjestä tietojoukko nousevaan järjestykseen.
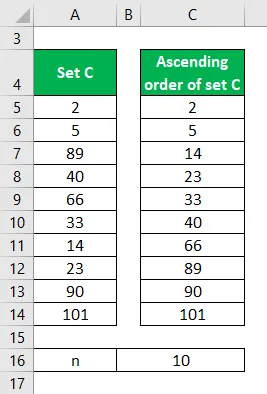
Mediaani lasketaan alla olevan kaavan avulla
Mediaani = (n + 1) / 2
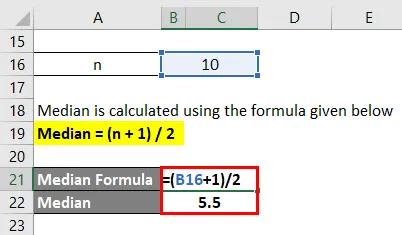
- Mediaani = (10 + 1) / 2
- Mediaani = 11/2
- Mediaani = 5, 5
5.5 on välillä 5–6. Joten meidän on otettava 5. ja 6. arvo tietojoukosta.
Yllä olevasta tietojoukosta 5. ja 6. arvo ovat vastaavasti 33, 40. Lisää molemmat luvut ja jaa kahdella saadaksesi mediaani. (33 + 40) / 2 = 73/2 = 36, 5. Joten tässä tämän tietojoukon mediaaniarvo on 36, 5 .
Esimerkki # 2.2:
Tarkastellaan suurta tietoryhmää D = 101, 102… 198.
Tämän tietojoukon kokonaismäärät ovat 98.
Täällä kokonaismäärät ovat 98. Joten n = 98.
Jaa nyt kokonaismäärät kahdella. Lisää ja vähennä 1 tuloksen arvosta. Tässä 98/2 = 49. Koska tämä on parillinen luku, keskiarvoja tulisi olla kaksi. Saatu mediaaniarvo on 49. Joten sillä pitäisi olla 48 numeroa mediaanin yläpuolella ja 48 numerolla mediaanin alapuolella. Siksi 49. ja 50. arvo ovat mediaaniarvoja.
Selitys
Vaihe 1: Järjestä ensin annettu tietojoukko nousevassa järjestyksessä. Sano, että sinulla on 4, 2, 8 ja 1 tietojoukko. Joten järjestämällä se nousevassa järjestyksessä saadaan 1, 2, 4, 8.
Vaihe 2: Tässä n on annetun tietojoukon alkioiden lukumäärä. Eli jos tarkastellaan yllä olevaa esimerkkitietojoukkoa 1, 2, 4 ja 8, muuttujan n arvo on 4.
Vaihe 3: Käytä muuttujan arvoa n kaavassa saadaksesi mediaani. eli mediaani = (n + 1) / 2
Vaikuttaa siltä, että tämä kaava on helppo nähdä, koska se on hyvin pieni tietojoukko. Mutta suurelle tietoryhmälle se vaatii enemmän ponnistuksia arvon saamiseksi oikein, koska vaiheet vaihtelevat vähän EVEN-numeromäärän ja ODD-määrän suhteen. Joten pitäisi olla hyvin varovainen etsiessäsi mediaania.
Tietojen lajittelujärjestys nousevassa järjestyksessä Excelissä
Excel-taulukossa oleva tietojoukko voidaan lajitella seuraavalla menetelmällä.
- Valitse solualue, jonka haluat lajitella. Sano, että sinulla on 1000 arvoa kokonaan ja se siirretään solusta A1 A1000.
- Siirry Tiedot-välilehteen -> Lajittele ja suodata ryhmä-> napsauta Lajittele. Tällöin voit lajitella tietojoukon pienimmästä luvusta korkeimpaan tai yksinkertaiseen. Voit napsauttaa hiiren kakkospainikkeella valittua data-aluetta ja valita lajitella -> Napsauta lajittelua pienimmästä suurimpaan numeroon.
Vaiheet tietokokonaisuuden laskemiseksi Excel-taulukossa, jotta saadaan n arvo suurelle tietoryhmälle
- Valitse solualue (joka on lajiteltu nousevassa järjestyksessä), jonka haluat laskea. Edellä olevan esimerkin mukaan se on A1: stä A1000: een.
- Siirry Kaavat-välilehteen -> napsauta Lisää toimintoja-> Osoita tilastollista ja valitse COUNTA-toiminto laskeaksesi solut, jotka eivät ole tyhjiä. Saat muuttujan n arvon. Tässä tapauksessa saat n = 1000.
Median-kaavan merkitys ja käyttö
Mediaaniarvo on tilastollinen mitta, jota käytetään monissa tosielämän skenaarioissa, kuten kiinteistöjen mediaanihinta, konkurssi-arvo jne. Tämä on erittäin hyödyllinen, kun tietojoukko sisältää erittäin korkeat ja matalat ryhmiteltyjen ja ryhmittelemättömien tietojoukkojen arvot. Mediaani on yksinkertaisesti kohta, jossa 50% yllä olevista numeroista ja 50% alla olevista numeroista. Se on vaistollinen keskittymä, joka kuvaa keskiarvoa. Tämä arvo on erittäin hyödyllinen, jos kyseessä on historiallinen tietojoukko tai tietojoukko, joka tulee ajan myötä.
Median Formula Laskin
Voit käyttää seuraavaa mediaanilaskuria
| n | |
| Mediaani kaava | |
| Mediaani kaava = |
|
|
Median kaava Excelissä (Excel-mallilla)
Tässä teemme uuden esimerkin Median-kaavasta Excelissä. Se on erittäin helppoa ja yksinkertaista.
Otetaan esimerkki mediaanin laskemiseksi.
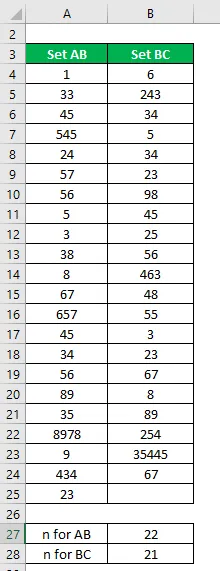
Järjestä tietojoukko nousevaan järjestykseen.

Mediaani lasketaan alla olevan kaavan avulla
Mediaani = (n + 1) / 2
Set AB: lle
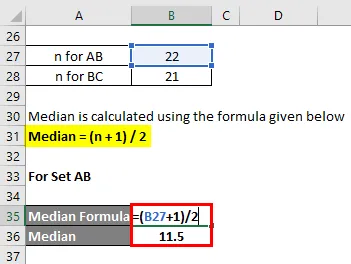
- Mediaani = (22 + 1) / 2
- Mediaani = 23/2
- Mediaani = 11, 5
Sarjalle BC
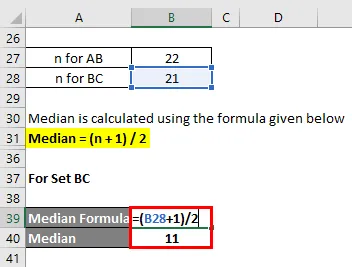
- Mediaani = (21 + 1) / 2
- Mediaani = 22/2
- Mediaani = 11
Suositellut artikkelit
Tämä on opas mediaani-kaavaan. Tässä keskustellaan kuinka lasketaan mediaani yhdessä käytännön esimerkkien kanssa. Tarjoamme myös Median-laskurin ladattavalla Excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Kuinka laskea keskiarvo kaavan avulla?
- Esimerkkejä DPMO-kaavasta
- Opas salkun variaatiokaavaan
- Kaava kestävälle kasvulle