Vektorit Matlabissa Vektoritoiminnan tyypit ja esimerkit

Johdanto vektoreihin Matlabissa

Vektori on suljettu joukko elementtejä. Matlabissa voimme luoda vektoreita hakasulkeilla. Vektorit ovat yksi esimerkkejä ryhmistä (yhden ulottuvuuden taulukko). sitä voidaan esittää kahdella tavalla rivivektori ja sarakevektori.

Rivivektori

Se on vaakasuora joukko elementtejä. Se on esitetty hakasulkeissa. Jokainen elementti erotetaan pilkulla tai välilyönnillä.

X = (4 7 8) tai X = (4, 7, 8)

Pylväsvektori

Se on pystysuora elementtijoukko. Se on esitetty myös hakasulkeissa. Sarakevektoreita voidaan luoda kahdella tavalla ensin erottamalla jokainen elementti puolipisteellä ja toinen tapa kirjoittaa jokainen elementti komentoikkunan seuraavalle riville.

X = (4; 6; 7) tai

X = (4

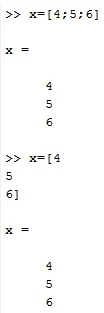
Vektoritoiminnot

Vektorioperaattorit luokitellaan laajasti kahteen luokkaan.

1. Aritmeettinen toiminta

Tarkastellaan kahta vektoria x ja y arvoilla x = (1 4 5 3) ja y = (5 3 2 1) voimme suorittaa erilaisia operaatioita näille kahdelle vektorille x ja y.

a. Kertolasku: Tätä toimintoa käytetään kertomalla aritmeettisella arvolla koko vektori.

Esimerkiksi:

mul = 3 * x

mul = 3 * (1 4 5 3)

mul = (3 12 15 9)

Syntaksi: variable name = arithmetic constant * vector name

b. Trigonometrinen toiminto: Voimme soveltaa mitä tahansa trigonometristä funktiota vektorimaiseen sin, cos, tan, cosec, sec jne.

Esimerkki tri = cos (x)

Vastaus on: 0, 54 - 0, 65 0, 28 -0, 99

Syntaksi: variable name = trigonometric function name ( vector name )

Summa: Tämä näyttää kokonaisten (lisättyjen) elementtien kokonaismäärän yhdessä vektorissa.

esimerkki

x = (1 4 5 3)

Yhteensä = summa (x)

Tuotos on yhteensä = 13

Syntaksi: variable name = = sum ( vector name )

C. Pituus: Se näyttää tietyn vektorin pituuden, olkoon yksi vektori p = (9 7 5 3 1 9 7 5 3 1)

esimerkki

p = (9 7 5 3 1 9 7 5 3 1)

Len = pituus (p)

Lähtö on Len = 10

d. Vektorien lisääminen: Kahden tai useamman vektorin lisääminen on yksinkertainen käyttö Matlabissa, tarkastellaanpa kahta vektoria p ja q.

P = (4 6 3 2) ja q = (5 7 9 1)

Lisää = p + q

Tuotos on Lisää = (9 13 12 3)

Syntaksi: vector name operator ( + ) vector name

Samoin voimme tehdä vähennystoimenpiteet kuten sub = p - q

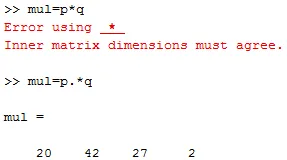
e. Vektorien kertolasku: Jos haluamme kertoa kaksi vektoria, yksinkertainen kertolaskutoiminto (*) ei toimi. Siksi meidän on lisättävä pisteoperaattori ('.') Kertolaskuoperaattorilla.

Esimerkki:

P = (4 6 3 2) ja q = (5 7 9 1)

mul = s. * q

lähtö on mul = (20 42 27 2)

Syntaksi: variable name = vector name dot operator multiplication operator vector name

Oletetaan, että haluan selvittää yhden tietyn vektorin neliön tai haluan kertoa vektorin vain tällä vektorilla.

Silloin syntaksi on squr = x. 2

2. Suhteellinen toiminta

a. Yhtä operaattoriin : tämä operaattori vertaa kutakin n jokaista elementtiä kahdesta vektorista ja antaa lähtö on nolla ja yksi muoto.

esimerkki

m = (2 5 8)

Ja n = (5 5 3)

Kuten tiedämme, vektorissa m ja vektorissa n on kolme elementtiä,

m == n

Yllä oleva lausuma antaa tuloksen 0 1 0, mikä tarkoittaa, että ensin ei ole yhtä suuri, toinen luku on sama ja kolmas ei ole yhtä suuri. O edustaa vääriä ja 1 tarkoittaa totta.

b. Alle operaattori (<): Alle operaattori edustaa symbolilla '<'. voimme verrata annettua matriisia mihin tahansa aritmeettiseen vakioon tai mihin tahansa muuhun vektoriin.

esimerkki

m = (3 2 4)

n = (1 1 1)

m <n

lähtö on 0 0 0, mikä tarkoittaa, että kaikki numerot ovat suuremmat kuin vektori n.

ja jos m <10

silloin lähtö on 1 1 1, mikä tarkoittaa, että kaikki numerot ovat alle 10.

C. Suurempi kuin operaattori (>): Suurempi kuin operaattori edustaa symbolilla ('>'). Voimme verrata annettua matriisia mihin tahansa aritmeettiseen vakioon tai mihin tahansa muuhun vektoriin.

Esimerkki:

M = (3 2 4)

N = (1 1 1)

m> n

Lähtö on 1 1 1, mikä tarkoittaa, että kaikki arvot ovat suuremmat kuin vektorin n arvot.

Johtopäätös - vektorit Matlabissa

Matlabissa voimme luoda erityyppisiä vektoreita, joissa pystymme suorittamaan erilaisia toimintoja, kuten summaus, vähennys, kertolasku, neliö, neliöjuuri, teho, skaalaus, vektorien kertolasku, pistekorjaus jne.

Suositellut artikkelit

Tämä on Matlabin vektoreiden opas. Tässä keskustellaan vektorioperaatioiden tyypeistä, joihin sisältyy aritmeettinen ja relaatioperaatio, sekä joitain esimerkkejä. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -