
Johdatus anonyymiin tehtäviin Matlabissa
Matlabissa on useita sisäänrakennettuja toimintoja (Matlabissa on saatavana erilaisia kirjastoja). Nämä sisäänrakennetut toiminnot tekevät Matlabista helpon ja tehokkaamman. Mutta jos haluamme luoda oman funktion, Matlabissa on yksi vaihtoehto, joka on toimintokahva. Funktion käsittelijän avulla voidaan luoda mikä tahansa matemaattinen funktio, joita kutsutaan anonyymeiksi funktioiksi.
Tarkastellaan yhtä esimerkkiä y = - 2, tässä on kaksi muuttujaa x ja y. x on tulo ja y on lähtö. Y: n arvo riippuu x: n arvosta.
Joten anonyymi funktionesitys on y = @ (x) 3 - 2
Yllä olevassa yhtälössä y on funktiokäsittelijä, x on syötemuuttuja ja '@' on anonyymiin toimintoihin käytetty symboli.
Tämän yhtälön kirjoittamisen jälkeen voimme antaa minkä tahansa arvon x. esimerkiksi y (0), y (1), y (2), y (3) jne
Jos x: n arvo on 0, niin y = x 3 - 2
Y = 0 - 2
Y = - 2
Samoin, jos x: n arvo on 1, niin y = 1 3 - 2
Y = 1 - 2
Y = -1
Vaiheet nimettömän funktion kirjoittamiseen Matlabiin
Vaihe 1: Määritä ensin Matlab-kahvatoiminto käyttämällä '@' -merkkiä ja syöttömuuttujaa, y = @ (x)
Vaihe 2: Kirjoita koko yhtälö funktiokäsittelymuuttujan viereen.
Vaihe 3: Hyväksy tuloarvo lähtömuuttujan sisällä, y (0).
Syntaksi:
Toiminnon määritelmä;
Toiminto;
Tarkastellaan yhtä yhtälöä p = q 2 - 3
| Matlab-koodi | Syntaksi |
| P = @ (q) | Toimintokahvan muuttuja = @ syöttömuuttuja |
| q 2 - 3 | Matemaattinen yhtälö |
| q (1) | Toimintokahvan muuttuja (syötemuuttujan arvo) |
Esimerkkejä anonyymeistä toiminnoista Matlabissa
Alla on erilaisia esimerkkejä nimettömästä toiminnosta Matlabissa seuraavasti:
Esimerkki # 1
Y = x 3 + 2x
Tässä esimerkissä näemme yksinkertaisen menetelmän nimettömästä toiminnosta.
Tässä Y on lähtö, x on muuttuva sisääntulo,
Jos laitamme x = 0
Y = 0 + 2 (0)
Y = 0
Jos laitamme x = 1
Y = x 3 + 2x
Y = 1 + 2
Y = 3
Jos laitamme x = 2
Y = x 3 + 2x
Y = 8 + 4
Y = 12
Jos laitamme x = 3
Y = x 3 + 2x
Y = 27 + 6
Y = 33

Matlab-koodi:
clc;
y = @ (x) x. 3 + (2 * x);
y (0)
y (1)
y (2)
y (3)
Yllä olevassa koodissa y ottaa arvot x käännöshetkellä. Näyttö 1 näyttää esimerkin 1 toteutuksen Matlabissa
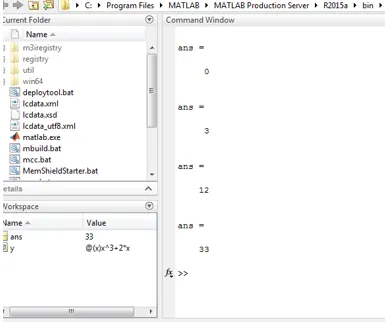
Esimerkki 2
y = x 3 - 2 * x + 3
jos x = 1
y = 1 - 2 + 3
y = 2
jos x = 2
y = 8 - 4 + 3
y = 7
jos x = 3
y = x 3 - 2 * x + 3
y = 27 - 6 + 3
y = 24

Matlab-koodi:
X = (1: 10)
y = @ (x) x. ^ 3 - 2 * x + 3
p = y (x)
juoni (y, x)
Yllä olevassa koodissa x vaihtelee välillä 0-10, joten 'x' -arvoja ei tarvitse määrittää käännöshetkellä. Jos x: n ja y: n diskreetit arvot ovat tiedossa, voimme piirtää muuttujan x ja y vastauksen. Näyttö 2 näyttää esimerkin 2 toteutuksen ja x: n ja y: n vastauksen.
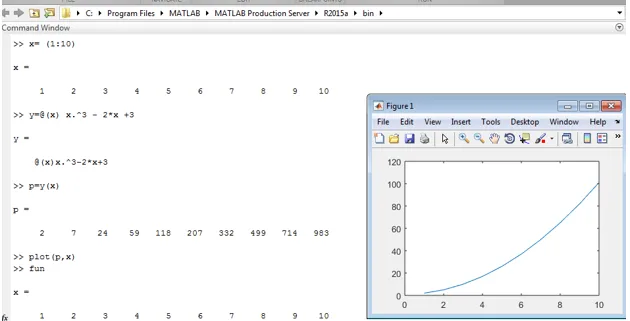
Esimerkki 3
Y = x 2 - loki (x)
Tässä esimerkissä on vaikea löytää logaritmia jokaiselle x: n arvolle. Matemaattisten laskelmien sijasta, jos käytämme suoria Matlab-komentoja, saadaan lähtö kaikilla y-arvoilla sekä x: n y-vastauksella (käyttämällä plot-komentoa). .

Matlab-koodi:
clc;
y = @ (x) x. 2 - loki (x)
y = @ (x) x. 2-loki (x)
x (1: 10)
p = y (x)
Yllä olevassa koodissa x vaihtelee välillä 0-10, joten 'x': n arvoja ei tarvitse määrittää käännöshetkellä ja jos x: n ja y: n diskreetit arvot ovat tiedossa, voimme piirtää muuttujan x ja y vastauksen. . Näyttö 2 näyttää esimerkin 2 toteutuksen ja x: n ja y: n vastauksen.
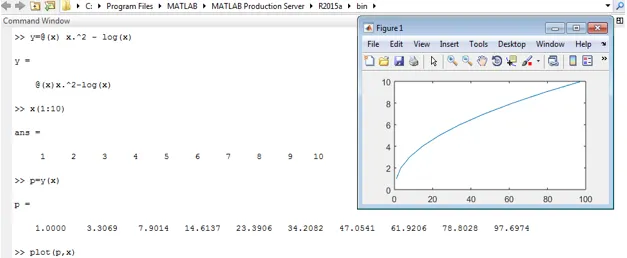
Anonyymien funktioiden edut Matlabissa
- Anonyymissä funktioissa voimme luoda minkä tahansa toiminnon, jota ei ole ennalta määritetty.
- Sitä voidaan tallentaa muuttujaan.
- Anonyymit toiminnot voidaan palauttaa toiminnossa.
- Se voidaan siirtää toiminnon sisällä.
- Näitä toimintoja ei voida tallentaa ohjelmatiedostoihin, joten voimme säästää muistia.
- Voimme tallentaa nimettömän toimintokahvan, jotta voimme käyttää sitä uudestaan ja uudestaan tarvittaessa.
- Sitä on helppo edustaa ja toteuttaa.
johtopäätös
Matlabissa anonyymejä funktioita käyttämällä voidaan helposti toteuttaa monimutkaiset matemaattiset neliö yhtälöt yksinkertaiseen muotoon. Näille toiminnoille ei ole määritetty nimeä, voimme antaa minkä tahansa nimen funktion määrittelyhetkellä. Anonyymi toiminto säästää muistia ja tukee uudelleenkäytettävyysominaisuutta, joten ei tarvitse kirjoittaa suurta ja monimutkaista lauseketta uudestaan ja uudestaan.
Suositellut artikkelit
Tämä on opas nimettömiin toimintoihin Matlabissa. Tässä keskustellaan Matlabin nimettömien funktioiden vaiheista ja eduista sekä joitain esimerkkejä. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Tietotyypit MATLABissa
- Kuinka asentaa MATLAB
- Matlab-komennot
- Matlabin käyttö
- Katsaus Matlabin rivitoimintoihin
- MATLAB-toiminnot
- Matlab-kääntäjä | Matlab-kääntäjän sovellukset