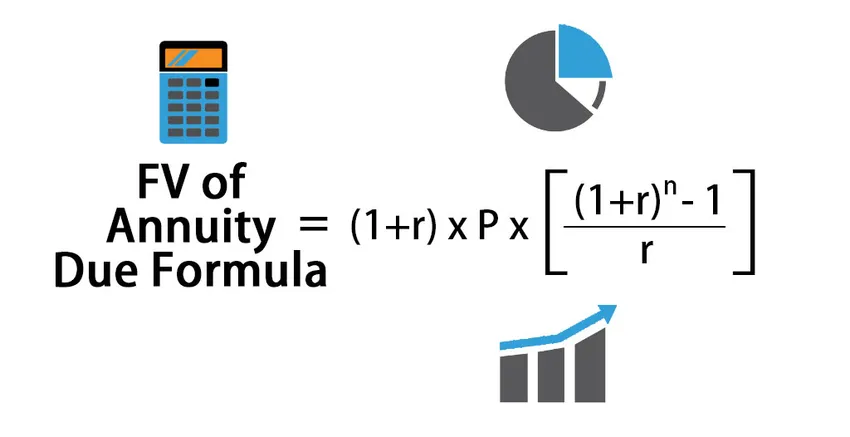
Eläkevakuutusmallin tuleva arvo (sisällysluettelo)
- Eläkevakuutusmallin tuleva arvo
- Esimerkkejä ansiosidonnaisen kaavan tulevaisuuden arvosta (Excel-mallilla)
- Eläkettä maksettavan kaavan laskin tulevaisuuden arvo
Eläkevakuutusmallin tuleva arvo
Kaava erääntyvien eläkkeiden tulevaisuuden arvon laskemiseksi:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Missä,
- P = Määräaikainen maksu
- R = ajanjakson hinta
- N = jaksojen lukumäärä
Esimerkkejä ansiosidonnaisen kaavan tulevaisuuden arvosta (Excel-mallilla)
Otetaan esimerkki ymmärtää paremmin laskettavan eläkkeiden tulevaisuuden arvon laskenta.
Voit ladata tämän eläkevakuutusmaksun tulevaisuuden arvon Formula Excel -malliin täältä - Eläkettä maksettavan eläkevakuuden tulevaisuuden arvo Formula Excel -malliEsimerkki # 1
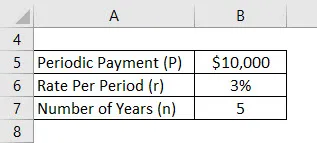
Oletetaan, että Anand on tallettanut 10 000 dollaria vuodessa ja hänen tilinsä tarjoama efektiivinen korko on 3%. Nyt Anand haluaa laskea tulevan saldonsa 5 vuoden kuluttua olettaen ensimmäisen talletuksen tänään.
Ratkaisu:
Erääntyvien eläkkeiden tulevaisuuden arvo lasketaan alla olevan kaavan avulla
Annuiteetin FV = (1 + r) * P * (((1 + r) n - 1) / r)
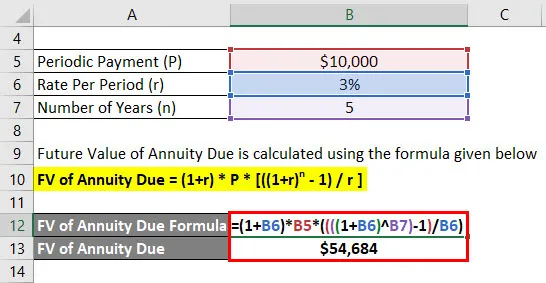
- Annuiteetin FV = (1 + 3%) * 10 000 dollaria * (((((1 + 3%) 5) - 1) / 3%)
- FV eläkemaksusta = 54 684 dollaria
Anandilla on tulevaisuuden saldo 54 684 dollaria viiden vuoden kuluttua.
Esimerkki 2
Oletetaan, että Jagriti on tallettanut 8000 dollaria vuodessa ja hänen tilinsä tarjoama efektiivinen korko on 5%. Nyt Jagriti haluaa laskea tulevan saldonsa 5 vuoden kuluttua olettaen, että ensimmäinen talletus otetaan tänään.

Ratkaisu:
Erääntyvien eläkkeiden tulevaisuuden arvo lasketaan alla olevan kaavan avulla
Annuiteetin FV = (1 + r) * P * (((1 + r) n - 1) / r)
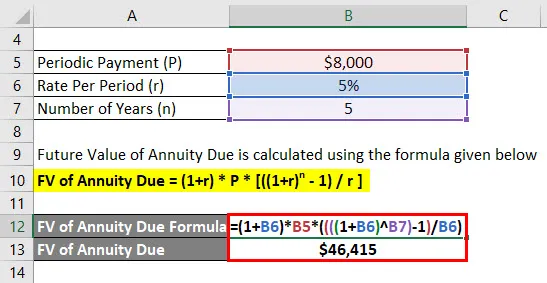
- Annuiteetin FV = (1+ 5%) * 8 000 $ * (((((1 + 5%) 5) - 1) / 5%)
- Annuiteetin FV = 46 415 dollaria
Jagriti saa tulevaisuuden saldon 46 415 dollaria 5 vuoden kuluttua.
Esimerkki 3
Oletetaan, että Anandriti on tallettanut 20 000 dollaria vuodessa ja hänen tilinsä tarjoama efektiivinen korko on 2%. Nyt Anandriti haluaa laskea tulevan saldonsa viiden vuoden kuluttua olettaen, että ensimmäinen talletus otetaan tänään.
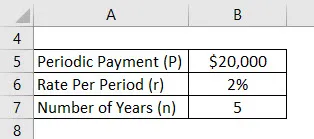
Ratkaisu:
Erääntyvien eläkkeiden tulevaisuuden arvo lasketaan alla olevan kaavan avulla
Annuiteetin FV = (1 + r) * P * (((1 + r) n - 1) / r)
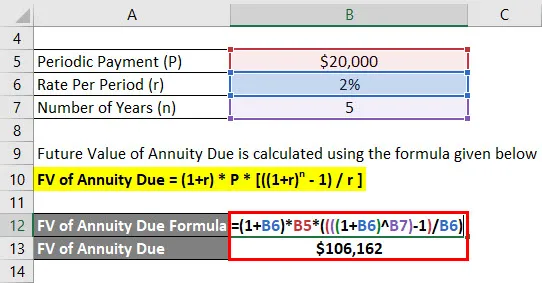
- Annuiteetin FV = (1+ 2%) * 20 000 dollaria * (((((1 + 2%) 5) - 1) / 2%)
- Annuiteetin FV = 1, 06 162 dollaria
Anandriti saa tulevan saldon 1 066 162 dollaria viiden vuoden kuluttua.
Selitys
Laskemme kassavirtasarjan tai maksusuorituksen loppuarvon, kun ensimmäinen erä saadaan välittömästi, käytämme erääntyvän annuiteetin tulevaisuuden arvoa. Ensimmäinen välitön erä tai maksu erottaa annuiteetin tavallisesta annuiteetista johtuen. Välitöntä tai välitöntä annuiteettia kutsutaan erääntyväksi annuiteetiksi.
Se laskee kassavirtojen arvon tulevana ajanjaksona. Erääntyvän annuiteetin FV: n käyttö on todellisissa tilanteissa erilainen kuin maksettavan annuiteetin nykyarvo. Oletetaan esimerkiksi, että yritys tai yksityishenkilö ostaa annuiteetin ja on maksanut ensimmäisen erän tänään. Voimme käyttää esimerkkiä selittämään tarkemmin, oletetaan, että yritys tai henkilö haluaa ostaa annuiteetin keneltä tahansa ja on suorittanut ensimmäisen maksun tänään. Voit laskea maksettavan hinnan tässä tilanteessa käyttämällä annuiteetin nykyarvon kaavaa. Jos kuitenkin haluamme laskea jäljellä olevan saldon sen jälkeen, kun tilille on tallennettu viiden vuoden korko, ja päätimme maksaa ensimmäisen erän tänään, käytetään tässä tapauksessa annuiteetin tulevaa arvoa. Erääntyvä annuiteetti voidaan selittää annuiteetin tyyppinä, jossa kassavirrat tapahtuvat kunkin jakson alussa. Kassavirtojen kehittyneen luonteen vuoksi jokaiselle kassavirralle on asetettu yhdistelmävaikutus jokaisesta lisäjaksosta, jos sitä verrataan tavanomaiseen annuiteettiin. Tavallisen annuiteetin tulevaisuuden arvo on alhaisempi kuin annuiteetin tuleva arvo, koska annuiteetin tulevaisuuden arvo saa määräajoin korkokertoimen yhden plus.
Määräisen annuiteetin tulevaisuuden arvon relevanssi ja käyttö
Ymmärretään erikseen tulevaisuuden arvon ja annuiteetin merkitys. Tulevaisuuden arvo voidaan selittää käteissuorituksen kokonaisarvolla, joka maksetaan tulevaisuudessa tietyllä päivämäärällä. Ja maksettava annuiteetti voidaan selittää maksusarjoina, jotka suoritetaan kunkin kauden alussa säännöllisessä järjestyksessä. Tästä syystä maksettavan annuiteetin tulevaisuuden arvo voidaan selittää tulevaisuuden kokonaisarvolla tiettynä ajankohtana systemaattisten / määräaikaisten maksujen sarjalle, jossa maksut suoritetaan kunkin kauden alussa. Tämän tyyppinen tapahtuma ja tällainen maksuvirta voidaan nähdä eläkeohjelman edunsaajatilillä. Kokonaisarvo on määrä, josta tulevaisuudessa suoritettavat maksusarjat kasvavat, koska tietyn koron määrän oletetaan olevan, ja ansiot kasvavat vähitellen tietyn ajanjakson aikana. Tavallisen annuiteetin tulevaisuuden arvon laskenta on identtinen tämän kanssa, mutta ainoa ero on, että lisäämme ylimääräisen maksuajan, joka tehdään alussa.
Eläkettä maksettavan kaavan laskin tulevaisuuden arvo
Voit käyttää seuraavaa eläkevakuutuslaskurin tulevaisuuden arvoa
| P | |
| R | |
| n | |
| Eläkevakuutusmallin tuleva arvo | |
| Eläkevakuutusmaksun tulevaisuuden arvo = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Suositellut artikkelit
Tämä on ollut opas eläkettä maksettavan kaavan tulevaisuuden arvoon. Tässä keskustellaan siitä, kuinka laskea maksettavan eläkevakuutuksen tulevaisuuden arvo käytännön esimerkkien avulla. Tarjoamme myös annuiteettisuunnitelman Future Value laskurin ladattavalla Excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Opas rahan aika-arvon kaavaan
- Esimerkkejä nykyarvokerroinkaavasta
- Laskurin tietosuhteen kaava
- Kaava käyttövipuasteelle