
Yhdistetty vuotuinen kasvunopeuskaava (sisällysluettelo)
- Kaava
- esimerkit
- Laskin
Mikä on yhdistetty vuotuinen kasvunopeuskaava?
Yhdistämisellä on vaikutusta, jossa sijoitus ei ansaitse korkoa pääkomponentista, vaan antaa myös korkoa. Joten yhdistetty vuotuinen kasvuvauhti on sijoituksille ansaittu efektiivinen vuotuinen kasvu ottaen huomioon sekoittuminen kuvaan. Tämä lähtökohtaisesti olettaa, että vuosittain ansaitut korot sijoitetaan uudelleen ja ne ansaitsevat saman koron kuin pääoma. Tästä syystä vuotuinen kasvuvauhti on aina korkeampi kuin yksinkertainen korko. Monet sijoitukset, kuten sijoitusrahastot, osakemarkkinoiden tuotot eivät ole kovin lineaarisia ja erittäin epävakaita.
Yhdistetty vuotuinen kasvuvauhti auttaa tasoittamaan tätä tuottoa ja kertoo kuinka paljon sijoittaja on ansainnut sijoituksen ajanjakson aikana, kun otetaan huomioon, että kaikki tuon ajanjakson väliset tuotot sijoitetaan uudelleen samaan hintaan. Tämän tasoittavan vaikutuksen takia se auttaa meitä vertaamaan tietojoukkoja erilaisella epävakaustasolla. Sitä käytetään hyvin usein taloudelliseen analyysiin.
Sijoituksen loppusumma = Alkusumma (1 + CAGR) Vuosien lukumäärä
Kaava yhdistettyyn vuotuiseen kasvuvauhtiin -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Tätä kaavaa voidaan käyttää, jos sijoitus kasvaa vuosittain, mikä tarkoittaa, että sijoitamme rahaa vuosittain. Mutta joskus tapahtuu, että haluamme laskea nopeuden, jolla yhdistyminen tapahtuu neljännesvuosittain, kuukausittain, päivittäin. Joten siihen käytämme seuraavaa kaavaa:
Päättyvän sijoituksen määrä = aloitusmäärä (1 + CAGR / yhdistelmätaajuus) (vuosien lukumäärä * yhdistelmätaajuus)
Joten, kaava yhdistetylle vuotuiselle kasvunopeudelle -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Yhdistämistaajuus:
- Puolivuotinen yhdistäminen: 2
- Neljännesvuosittain yhdistäminen: 4
- Kuukausittain: 12 ja niin edelleen
Esimerkkejä CAGR-kaavasta (Excel-mallilla)
Otetaan esimerkki ymmärtääksesi CAGR-kaavan laskentaa paremmin.
Voit ladata tämän yhdistetyn vuosikasvun Excel-mallin täältä - Yhdistetyn vuotuisen kasvunopeuden Excel-mallinCAGR-kaava - esimerkki # 1
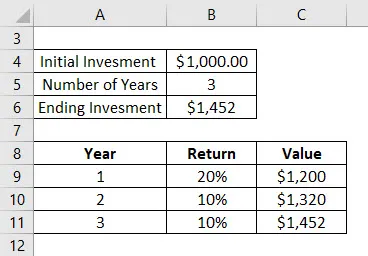
Oletetaan, että olet sijoittanut 1000 dollaria sijoitusrahastoihin 3 vuotta sitten. Seuraava on paluu, jonka sait näiden 3 vuoden aikana:
- Ensimmäisenä vuonna arvonnousu oli 20%. Joten kokonaisarvo on 1200 dollaria ensimmäisen vuoden lopussa
- 2. vuosi saat arvonnousun 10%. Joten kokonaisarvo on toisen vuoden lopussa 1320 dollaria
- Kolmas vuosi, saat arvonnousun 10%. Joten kokonaisarvo on 1452 dollaria 3. vuoden lopussa
CAGR lasketaan alla olevan kaavan avulla
CAGR = (lopullinen sijoitusmäärä / aloitusmäärä) (1 / vuosien lukumäärä) - 1
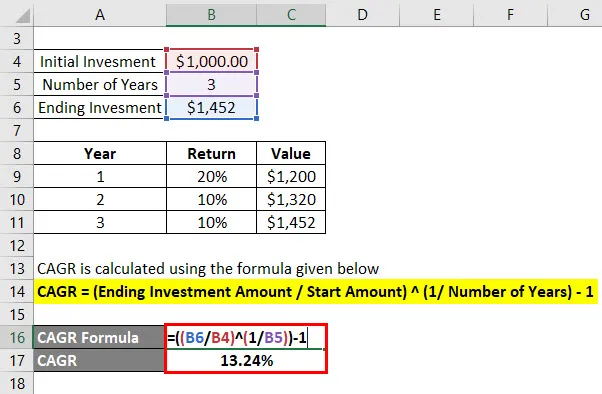
- CAGR = (1 452 dollaria / 1 000 dollaria) (1/3) - 1
- CAGR = 13, 24%
Täällä voimme nähdä, että kaikkien 3 vuoden vuotuinen tuotto on erilainen ja vaihteleva, mutta yhdistetty vuotuinen kasvuvauhti antaa meille yhden koron, jota voimme verrata erilaisiin sijoitusmahdollisuuksiin.
CAGR-kaava - esimerkki 2
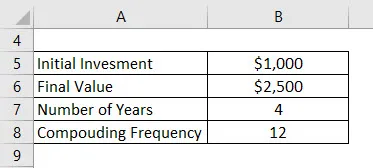
Oletetaan, että olet sijoittanut 1000 dollaria pankkiin ja haluat pitää rahaa pankissa 4 vuotta. Sanotaan nyt, että kokonaismäärä, jonka saat 4 vuoden kuluttua, on 2500 dollaria. Pankki tarjoaa koron kuukausittain laskemalla. Laske CAGR.
CAGR lasketaan alla olevan kaavan avulla
CAGR = yhdistelmätaajuus * ((lopullinen sijoitusmäärä / aloitusmäärä) (1 / (vuosien lukumäärä * yhdistelmätaajuus)) - 1)
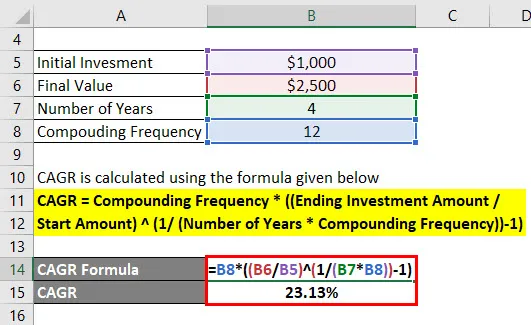
- CAGR = 12 * ((2 500 dollaria / 1 000 dollaria) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Joten yhdistetty vuotuinen kasvuvauhti on 23, 13%.
Selitys yhdistetystä vuotuisesta kasvunopeuskaavasta
Vaikka yhdistetty vuotuinen kasvuvauhti on investoinnin vuotuinen korko, se on vain teoreettinen luku eikä ole todellinen tuotto. Tärkein oletus tässä on, että kaikki ansiot sijoitetaan uudelleen samaan korkoon sijoituskaudella, mutta korko ei pysy kaikkien vuosien ajan, emmekä välttämättä sijoita rahaamme samaan hintaan. Joten se on ainoa edustava kurssi, joka kertoo meille, että mitä voimme saada aikaan, jos kaikki rahat sijoitetaan uudelleen jokaisen vuoden lopussa tällä kurssilla. Joten on joitain avainkysymyksiä, jotka meidän tulisi ottaa huomioon käytettäessä yhdistettyä vuotuista kasvuvauhtia.
Lisäksi olemme todella varovaisia sijoituksen suhteen, joka on pitkä jakso. Esimerkiksi, jos sijoituskausi on erittäin pitkä, esimerkiksi 20 vuotta, yhdistetty vuotuinen korko saattaa antaa meille väärän viitteen, koska voi tapahtua, että emme ansaitse voittoa ensimmäisen 15 vuoden aikana ja kaikki tuotot tulevat viimeiseltä kaudelta . Voiton ansaitseminen 15 vuoden ajan ei ole hyväksyttävää minkään liiketoiminnan kannalta.
Samoin, jos kahdella sijoitusmahdollisuudella on sama CAGR, voi olla niin, että toinen houkuttelee enemmän kuin toinen, koska yhdessä kasvu tapahtuu alkujaksolla, kun taas toisessa kasvu keskittyy sijoitusrahastojen loppuun. aikana.
Yhdistetyn vuotuisen kasvunopeuskaavan relevanssi ja käyttö
Yhdistelty vuosikasvu on todella hyödyllinen sijoituksen keskimääräisen kasvun laskemisessa ja voi auttaa eri sijoitusten vertailussa. Kuten olemme nähneet yllä olevasta esimerkistä, investointien kasvu on epätasaista ja epätasaista vuosittain. Mutta käyttämällä yhdistettyä vuosikasvua, tuotto tasoittuu. Toinen tekijä, joka tekee yhdistetystä vuotuisesta kasvunopeudesta kriittisen menetelmän sijoituksen kasvun määrittämisessä, on se, että se ottaa huomioon yhdistelmävaikutuksen, mikä ei aiheuta vuotuista tuottoa. Yhdistetty vuotuinen korko ei anna meille todellista kuvaa tuotosta, koska se laskee vain pääoman tuoton ja jättää huomiotta korkokomponentin koron, mutta näin ei ole tilanne yhdistetyn vuosikasvun tapauksessa.
Yhdistetty vuotuinen kasvunopeuskaavalaskin
Voit käyttää seuraavaa yhdistettyä vuotuista kasvunopeuslaskuria
| Päättyvä sijoitusmäärä | |
| Aloitusmäärä | |
| Vuosien lukumäärä | |
| CAGR | |
| CAGR = | ((Lopullinen sijoitusmäärä / aloitusmäärä) 1 / vuosien lukumäärä -1) |
| = | ((0/0) 1/0 -1) = 0 |
Suositellut artikkelit
Tämä on opas yhdistettyyn vuotuiseen kasvunopeuskaavaan. Tässä keskustellaan siitä, kuinka CAGR voidaan laskea, sekä käytännön esimerkkejä. Tarjoamme myös yhdistetyn vuotuisen kasvunopeuslaskurin ladattavalla excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Opas tuottoprosentin kaavaan
- Esimerkkejä eksponentiaalisesta kasvusta
- Laskin keskimääräiselle rajalauseelle
- Kuinka laskea markkina-arvo?