Poisson-jakauma Excelissä (sisällysluettelo)
- Yleiskatsaus Poissonin jakelufunktioon Excelissä
- Kuinka käyttää Poisson-jakautumistoimintoa Excelissä?
Yleiskatsaus Poissonin jakeluun Excelissä
Seuraava Poisson-jakauma Excelissä antaa yleiskuvan Excelissä yleisimmin käytetyistä toiminnoista. Se on valmiiksi integroitu integroitu todennäköisyysjakamisfunktio (pdf), joka luokitellaan tilastollisiin toimintoihin.
Sitä käytetään tuloennusteiden laskemiseen.
Se liittyy eksponentiaaliseen jakautumiseen. Se on tapahtuman esiintymisten määrä tietyllä aikayksiköllä, etäisyydellä, alueella tai tilavuudella, esim
a) Pyöräonnettomuuksia ei ole tapahtunut päivässä. Tässä tapahtuman esiintymisten lukumäärä on Poissonin satunnaismuuttuja, se on arvaamattoman & tuntematon, tapahtumat tapahtuvat satunnaisesti ja itsenäisesti.
b) Puhelinsoittojen lukumäärä, jonka puhelinkeskuksen edustaja on vastaanottanut 60 minuutin kiinteänä ajanjaksona.
c) Virheiden lukumäärä kangaspultissa.
d) Virheiden lukumäärä asiakirjan jokaisella sivulla, jotka voivat olla oikeinkirjoitus- tai muita virheitä.
Poisson-todennäköisyysmassofunktio laskee x-tapahtumien todennäköisyyden ja se lasketaan alla mainitulla tilastollisella kaavalla:
P (x, λ) = ((e −λ ) * λ x ) / x!
Tässä,
- λ (Lambda) on odotettu tapahtumien määrä määrätyn ajanjakson aikana.
- X: n (satunnaismuuttuja) sanotaan olevan Poissonin satunnaismuuttuja parametrilla λ.
- e on samanlainen kuin pi, on matemaattinen vakio, luonnollisten logaritmien emäs, joka on suunnilleen yhtä suuri kuin 2.71828.
- x! jota kutsutaan x-tekijäksi, esimerkiksi viisi tekijää olisi 120, joka lasketaan
5! = 5x4x3x2x1 = 120
Huomaa: Tässä satunnaismuuttujan keskiarvo on yhtä suuri kuin lambda, lambdaa käytetään usein Poisson-jakaumassa.Poisson-jakaumakäyrät todennäköisyysmassille ja kumulatiiviselle
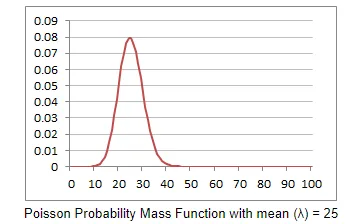
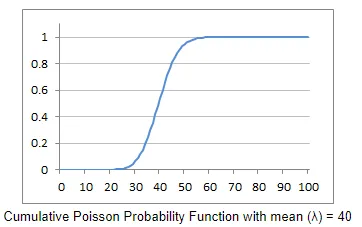
Poisson-jakautumistehtävän selitys Excelissä
Sitä käytetään arvioimaan tai ennustamaan tietyn määrän tapahtumien esiintymisen todennäköisyyttä tietyn ajanjakson tai tilan sisällä.
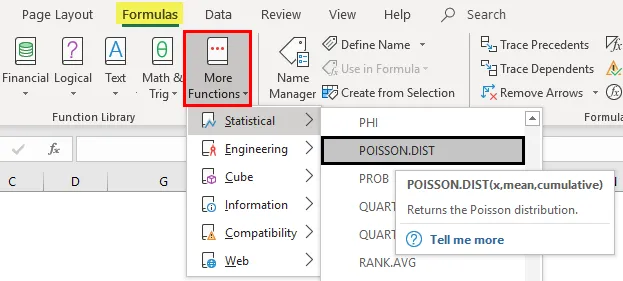
Poisson-jakelutoiminnon syntaksi tai kaava Microsoft Excelissä on:

POISSON.DIST-toiminnon syntaksilla tai kaavalla on seuraava argumentti:
- x: se on niiden tapahtumien kokonaismäärä, joiden tapahtumien todennäköisyys lasketaan.
Tämän arvon tulisi olla kokonaisluku; Jos desimaali toimitetaan, Excel katkaisee sen kokonaislukuun.
- Keskiarvo : odotettu tapahtumien lukumäärä (Huomaa: sen on oltava ≥ 0).
- Kumulatiivinen : Looginen argumentti, joka määrittelee laskettavan jakauman tyypin.
Tässä voi olla jakautumisen tyyppi tai se voi olla jompikumpi alla mainituista:
- TOSI tai 1 - Käytä kumulatiivista jakautumistoimintoa tai
Se palauttaa tapahtuman x tai vähemmän tapahtuvan kumulatiivisen todennäköisyyden.
- FALSE tai 0 - Käytä todennäköisyysmassa- tai tiheysfunktiota.
eli Excel palauttaa todennäköisyyden vain x tapahtumien lukumäärästä.
Kuinka käyttää Poisson-jakautumistoimintoa Excelissä?
Tarkastellaan esimerkkejä siitä, kuinka Poisson Distribution -toiminto toimii Excelissä.
Voit ladata tämän Poisson Distribution Excel -mallin täältä - Poisson Distribution Excel TemplateEsimerkki 1 - todennäköisyysmassien tai tiheysfunktioiden laskeminen
Oletetaan, että lähtevän puhelinkeskuksen edustajalla on soitettu 5, 8 puhelinsoittoa minuutissa, tässä puhelujen esiintyminen voidaan ennustaa POISSON-jakelun kautta tai sen avulla. Katsotaanpa kuinka laskea sekä kumulatiivinen jakelufunktio että todennäköisyysmassa- tai tiheysfunktio.
Nyt voimme laskea todennäköisyysmassa- tai tiheysfunktion Poisson-jakauman funktion avulla.
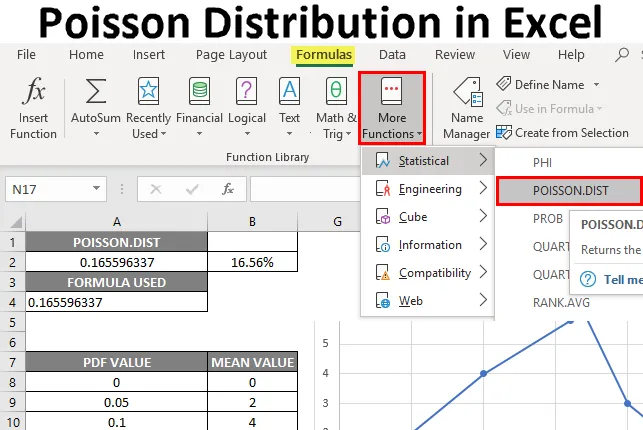
- Valitse solu, johon Poisson Distribution Function -toimintoa on käytettävä kumulatiivisen jakauman laskemiseksi , ts. “A2”
- Napsauta nyt lisäystoimintopainiketta (fx) kaavatyökalurivin alla excel-arkin yläreunassa. Nyt ilmestyy valintaikkuna, jossa sinun pitäisi kirjoittaa avainsana ”POISSON” etsittäessä toimintokenttää. Kaksi tyyppiä Poisson-yhtälöitä ilmestyy. Tässä sinun on valittava Poisson Distribution -toiminto.
Oletetaan, että puhelinkeskuksen edustaja soitti tarkalleen 5 puhelinsoittoa 1 minuutissa.
X = 5, se on niiden tapahtumien kokonaismäärä, joiden tapahtumien todennäköisyys lasketaan.
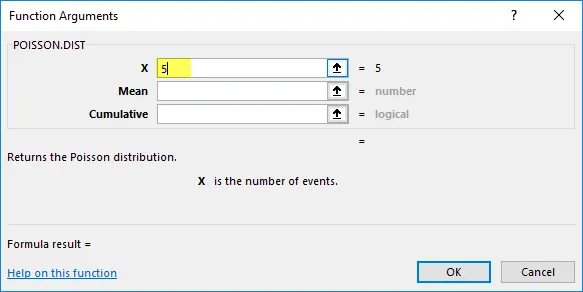
Keskiarvo = 5, 8, se on odotettu tapahtumien lukumäärä.
Kumulatiivinen : Looginen argumentti, joka määrittelee laskettavan jakauman tyypin.
- Tässä selvitettävä jakauman tyyppi on todennäköisyysmassa- tai tiheysfunktio. siksi kumulatiivinen = väärä tai 0 (todennäköisyystiheysfunktio). Se palauttaa todennäköisyyden vain x tapahtumien lukumäärästä.
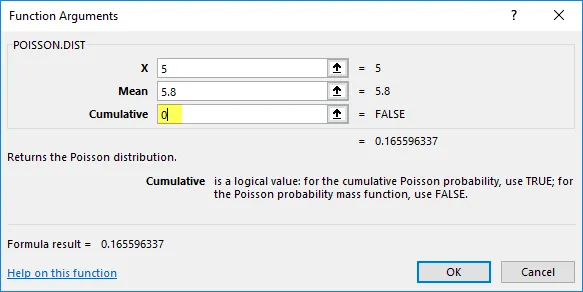
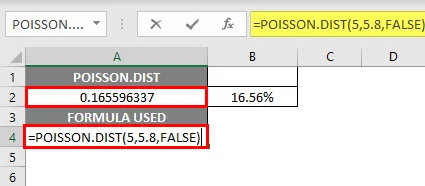
- Poisson Distribution-funktio palauttaa todennäköisyysmassan tai tiheysfunktion arvon, ts. 0.165596337, missä sinun on muutettava se prosenttimääräksi, mikä johtaa 16, 55%.
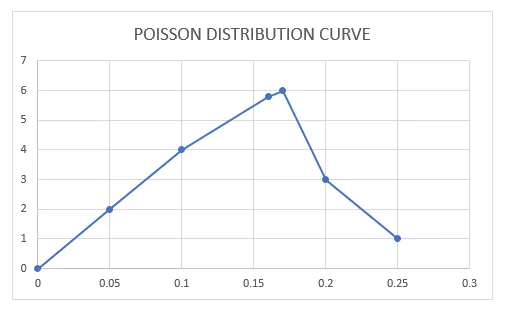
Edellä esitetyn arvon kanssa, jos piirrän kuvaajan todennäköisyysmassan tai tiheyden funktion suhteen, ts. Puheluita minuutissa Y-akselilla (keskiarvot) ja todennäköisyysmassan tai tiheyden arvon X-akselilla (Pdf-arvot), se näyttää mainitulla tavalla alla.
Poisson-jakaumakäyrä todennäköisyysmassan tai tiheyden funktion suhteen
Samoin voimme laskea kumulatiivisen jakauman Poisson Distribution -funktion avulla.
Esimerkki 2 - Kumulatiivisen jakauman laskeminen
Oletetaan, että puhelinkeskus on soittanut jopa 5 puhelua minuutissa.
Kumulatiivisen jakauman laskemiseksi Poisson Distribution -toiminnon avulla ainoa muutos, joka on tehtävä, on Poisson Distribution -toiminnon kumulatiivinen argumentti, joka on asetettu TRUE-arvoksi väärän sijaan.
- Valitse solu, johon Poisson Distribution Function -toimintoa on käytettävä kumulatiivisen jakauman laskemiseksi, ts. “D6”
- Napsauta nyt lisäystoimintopainiketta (fx) kaavatyökalurivin alla excel-arkin yläreunassa. Nyt ilmestyy valintaikkuna, jossa sinun pitäisi kirjoittaa avainsana “POISSON” etsiessäsi toimintokenttää. Näkyviin tulee kaksi tyyppiä Poisson-yhtälöitä. Tässä sinun on valittava Poisson Distribution -toiminto.
Oletetaan, että puhelinkeskuksen edustaja soitti tarkalleen 5 puhelinsoittoa 1 minuutissa.
X = 5, se on niiden tapahtumien kokonaismäärä, joiden tapahtumien todennäköisyys lasketaan
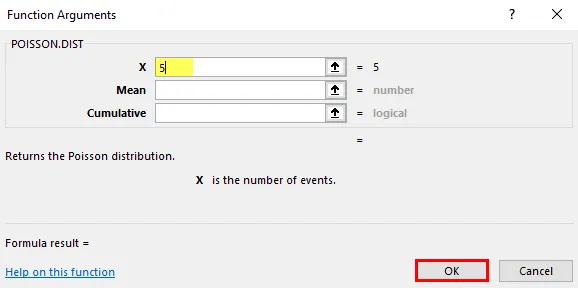
Keskiarvo = 5, 8, se on odotettu tapahtumien lukumäärä.
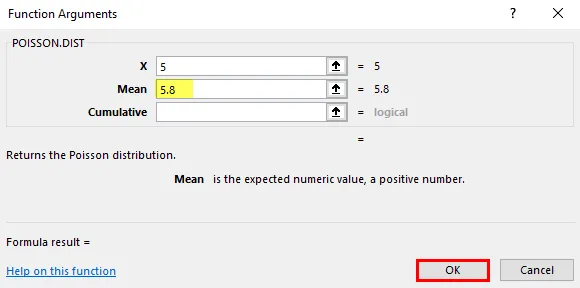
Kumulatiivinen : Looginen argumentti, joka määrittelee laskettavan jakauman tyypin.
Täällä selvitettävä jakelu on KUMULATIIVINEN. Siksi kumulatiivinen = Tosi tai 1 Kumulatiivinen tiheysfunktio (CDF).
Excel palauttaa tapahtuman x tai vähemmän tapahtuvan kumulatiivisen todennäköisyyden.
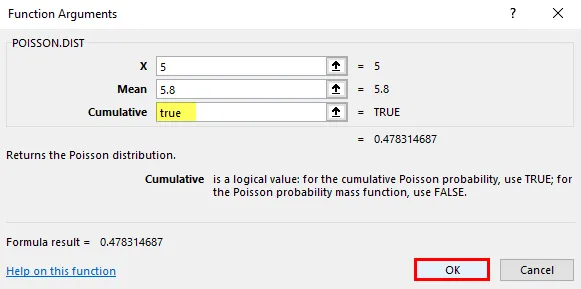
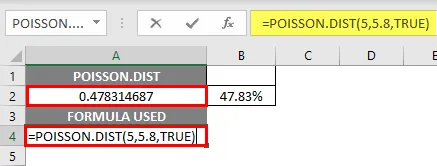
Poisson Distribution-funktio palauttaa kumulatiivisen jakauman arvon eli 0, 478314687, missä sinun on muunnettava se prosenttiosuudeksi, mikä johtaa 47, 83%.
Muistettavat asiat
- Jos X: n arvo tai keskiarvo on pienempi kuin nolla Poisson Distribution -toiminnossa, tapahtuu #NUM-virhe.

- Jos jokin Poisson Distribution -toiminnon perusteista ei ole numeerinen, niin #VALUE! virhe

- Poisson-jakautumistoiminnon X-arvon tulisi aina olla kokonaisluku, jos syötät desimaalin arvon, Excel katkaisee sen kokonaisluvuksi
Suositellut artikkelit
Tämä on opas Poisson Distributioniin Excelissä. Tässä keskustellaan siitä, kuinka Poisson-jakelutoimintoa käytetään Excelissä, sekä esimerkkejä ja ladattavaa Excel-mallia. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- DAY-kaava Excelissä
- Sarakkeet Excel-kaava
- VALITSE kaava Excelissä
- Hakutaulukko Excelissä