
Johdatus DFS-algoritmiin
DFS tunnetaan nimellä Depth First Search Algorithm, joka tarjoaa vaiheet graafin jokaisen solmun kuljettamiseksi toistamatta mitään solmua. Tämä algoritmi on sama kuin puun syvyyden ensimmäinen läpikäynti, mutta eroaa siinä, että ylläpidetään loogista tarkistaa, onko solmuun jo käyty vai ei. Tämä on tärkeää kuvaajan kulkemiselle, koska jaksossa on myös jaksoja. Tässä algoritmissa ylläpidetään pino ripustettujen solmujen tallentamiseksi poikittaisen ajan. Sille on annettu nimi, koska matkustamme ensin jokaisen viereisen solmun syvyyteen ja jatkamme sitten toisen viereisen solmun kuljettamista.
Selitä DFS-algoritmi
Tämä algoritmi on vastoin BFS-algoritmia, jossa kaikki vierekkäiset solmut käyvät vierekkäisten solmujen naapureiden seurassa. Se alkaa tutkia kuvaajaa yhdestä solmusta ja selvittää sen syvyyttä ennen takaisinottoa. Tässä algoritmissa otetaan huomioon kaksi asiaa:
- Käynti Vertexissä: Kaavion kärjen tai solmun valinta kulkemaan.
- Vertexin etsintä: Kaikkien kyseisen kärjen vieressä olevien solmujen läpi kulkeminen.
Pseudokoodi syvälle ensimmäiselle haulle :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Lineaarista läpikulkua on myös DFS: lle, joka voidaan toteuttaa kolmella tavalla:
- Ennakkotilaus
- Järjestyksessä
- postorder
Käänteinen postinvaihto on erittäin hyödyllinen tapa kulkea ja sitä käytetään topologisessa lajittelussa sekä erilaisissa analyyseissä. Pinoa ylläpidetään myös niiden solmujen tallentamiseksi, joiden etsintä on vielä kesken.
Graafin kulku DFS: ssä
DFS: ssä seuraavia vaiheita seurataan käyrän läpi. Esimerkiksi annettu graafi, aloittakaamme kulku 1: stä:
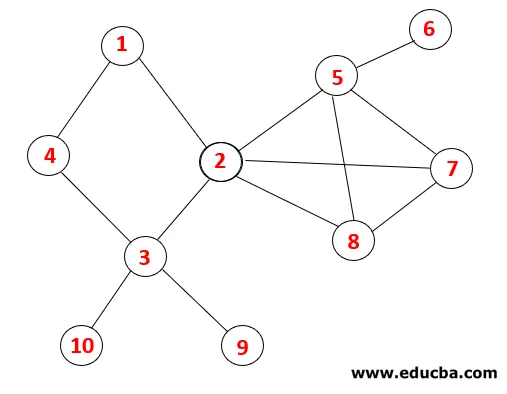
| Pino | Läpikulkujakso | Kattaa puun |
| 1 |  |
|
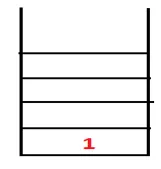 | 1, 4 |  |
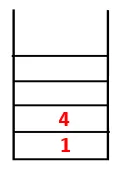 | 1, 4, 3 |  |
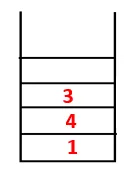 | 1, 4, 3, 10 | 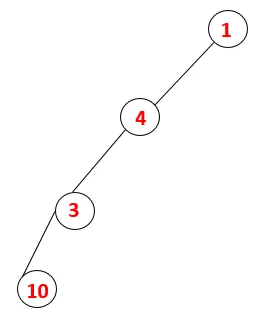 |
 | 1, 4, 3, 10, 9 | 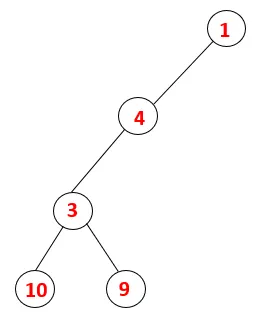 |
 | 1, 4, 3, 10, 9, 2 | 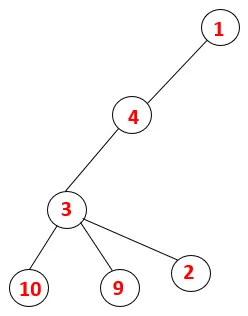 |
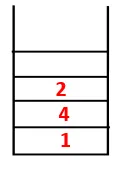 | 1, 4, 3, 10, 9, 2, 8 |  |
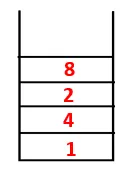 | 1, 4, 3, 10, 9, 2, 8, 7 | 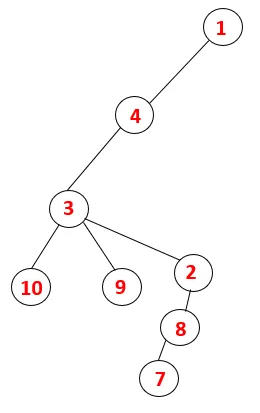 |
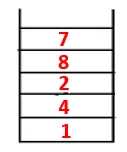 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
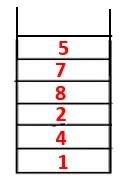 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 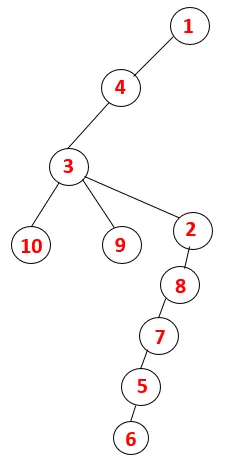 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 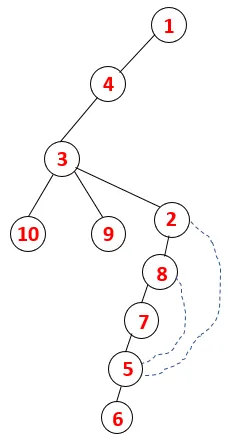 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
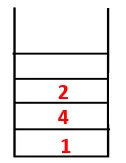 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 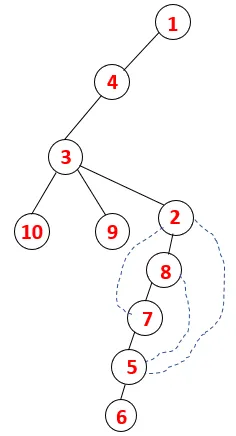 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 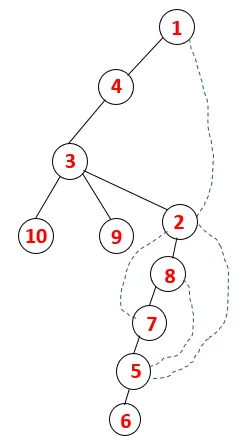 |
Selitys DFS-algoritmiin
Alla on vaiheet DFS-algoritmiin, jolla on edut ja haitat:
Vaihe 1: Solmua 1 käydään ja lisätään sekvenssiin samoin kuin kattava puu.
Vaihe 2: 1 vierekkäisiä solmuja tutkitaan, mikä on 4, siten 1 työnnetään pinoon ja 4 työnnetään sekvenssiin samoin kuin ulottuva puu.
Vaihe 3: Yhtä 4: n viereisistä solmuista tutkitaan ja siten 4 työnnetään pinoon, ja 3 tulee sekvenssi- ja ulottuvaan puun.
Vaihe 4: 3 : n vierekkäiset solmut tutkitaan työntämällä se pinoon ja 10 siirtyy sekvenssiin. Koska 10: llä ei ole viereistä solmua, siis 3 aukeaa pinosta.
Vaihe 5: Toista vierekkäistä 3 solmua tutkitaan ja 3 työnnetään pinolle ja 9 käydään. Mitään vierekkäistä solmua 9, siten 3, ei popp ulos ja viimeistä viereistä solmua 3 eli 2 käydään.
Samanlaista prosessia noudatetaan kaikissa solmuissa, kunnes pino tyhjenee, mikä osoittaa läpikulkualgoritmin pysäytysolosuhteet. - -> Katkoviivalla katkoviivat viittaavat kuvaajan takareunoihin.
Tällä tavalla kaikki kuvaajan solmut kulkevat toistamatta mitään solmuja.
Hyödyt ja haitat
- Edut: Tämä algoritmin muistivaatimus on hyvin vähäinen. Vähemmän tilaa ja aikaa monimutkaisia kuin BFS.
- Haitat: Ratkaisua ei taata Sovellukset. Topologinen lajittelu. Graafin siltojen löytäminen.
Esimerkki DFS-algoritmin toteuttamisesta
Alla on esimerkki DFS-algoritmin toteuttamiseksi:
Koodi:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
lähtö:
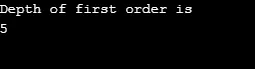
Selitys yllä olevaan ohjelmaan: Teimme kuvaajan, jossa oli 5 kärkipistettä (0, 1, 2, 3, 4), ja käyimme käytetyn taulukon avulla kaikkien käyneiden kärkien seurantaa. Sitten jokaiselle solmulle, jonka vierekkäiset solmut ovat olemassa, sama algoritmi toistuu, kunnes kaikki solmut käyvät. Sitten algoritmi palaa takaisin kärkipisteeseen ja popin se pinosta.
johtopäätös
Tämän kuvaajan muistivaatimus on vähemmän verrattuna BFS: ään, koska vain yksi pino on ylläpidettävä. Tuloksena syntyy DFS: n ulottuva puu ja läpikulkujakso, mutta se ei ole vakio. Useita poikkisuuntaisia sekvenssejä on mahdollista valitusta aloitus- ja tutkimuspisteestä riippuen.
Suositellut artikkelit
Tämä on opas DFS-algoritmiin. Tässä keskustellaan askel askeleelta selittämisestä, siirrytään kuvaajaan taulukkomuodossa etujen ja haittojen kanssa. Voit myös käydä läpi muiden aiheeseen liittyvien artikkeleidemme saadaksesi lisätietoja -
- Mikä on HDFS?
- Syvän oppimisen algoritmit
- HDFS-komennot
- SHA-algoritmi