Excel NORMSINV (Sisällysluettelo)
- Johdanto Excel NORMSINV -sovellukseen
- Kuinka käyttää NORMSINV-kaavaa Excelissä?
Johdanto Excel NORMSINV -sovellukseen
Käänteisen normaalin kumulatiivisen jakauman funktio excelissä on tärkeä työkalu, joka palauttaa käänteisen normaalin kumulatiivisen jakauman tietylle todennäköisyysarvolle, ts. Se yleensä palauttaa käänteisen normaalille normaalille kumulatiiviselle jakautumiselle (jonka keskiarvo on nolla ja keskihajonta yksi) NORM.S.INV-toiminto esiteltiin ensin Microsoft Excel -versiossa 2010, joka on päivitetty versio NORMSINV-toiminnosta excel 2013: ssa ja viimeisin versio. NORMSINV-toimintoa käytetään enimmäkseen ostoveloissa ja talousanalyysissä.
Excel NORMSINV: n syntaksi

Perustelu:
Todennäköisyys - Mikä on vain todennäköisyys, vastaa normaalia jakaumaa.
Kuinka käyttää NORMSINV-kaavaa Excelissä?
Microsoft excel -sovelluksessa sisäänrakennettu NORMSINV-toiminto luokitellaan tilastofunktioon, joka esitetään alla olevassa kuvakaappauksessa (missä se laskee normaalin kumulatiivisen jakauman käänteisen tietylle todennäköisyydelle).
- Siirry Kaavojen valikkoon.
- Napsauta Lisää toiminto alla olevan kuvakaappauksen osoittamalla tavalla.

- Valitse tilastoluokka, josta löydät NORM.DIST-toiminnon, kuten alla on esitetty.
Esimerkki 1 - NORM.DIST: n ja NORMSINV: n käyttö
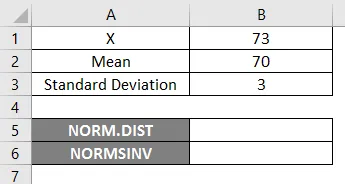
Jotta voisimme käyttää NORM.DIST-toimintoa, aloitetaan helposta esimerkistä, jossa meidän on selvitettävä opiskelijoiden arvosanat. Oletetaan, että meillä on luokan tentti, jonka keskimääräinen arvosana on 70 eli mu = 70 ja luokan keskihajonta on 3 pistettä eli sigma = 3 tässä meidän on selvitettävä, mikä on todennäköisyys, että opiskelijat saivat arvosanat 73 tai vähemmän eli P (X <= 73). Joten katsotaan kuinka selvittää todennäköisyys NORM.DIST-toiminnon avulla.
- X = 3
- Keskiarvo = 70
- Vakiopoikkeama = 3
- Käytä NORM.DIST-toimintoa kuten alla.
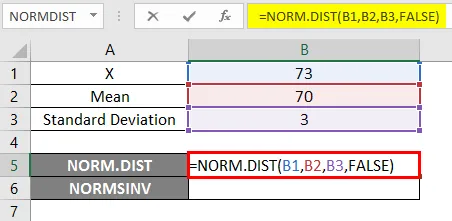
- Jos sovellamme yllä olevaa NORM.DIST-funktiota, saamme todennäköisyyden 0.0807.
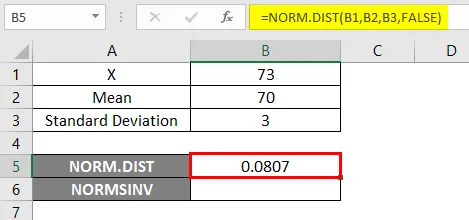
- Käytä nyt NORMSINV-toimintoa selvittääksesi normaalin kumulatiivisen jakauman käänteisen kuvan alla.
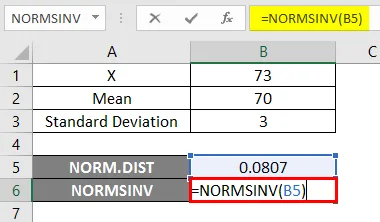
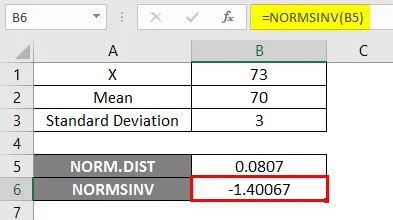
Tulos -
Alla olevassa tuloksessa voimme nähdä, että saimme negatiiviset arvot -1.40067 annetulle todennäköisyydelle eli normaalin kumulatiivisen jakauman käänteiseksi.
Esimerkki 2 - keskimääräinen ja tarkka keskihajonta
Katsotaan toinen esimerkki käyräpohjaisilla tiedoilla, jotta voimme tutustua keskiarvoon ja tarkkaan standardipoikkeaman.
- Keskiarvo = 7
- Vakiopoikkeama = 1.3
- Vakiopoikkeaman lisäys asteikolla -3

- Kellokäyrän saamiseksi meidän on lisättävä 0, 1 vakiopoikkeaman lisäykseen, jos tiedot ovat alla esitetyllä tavalla.
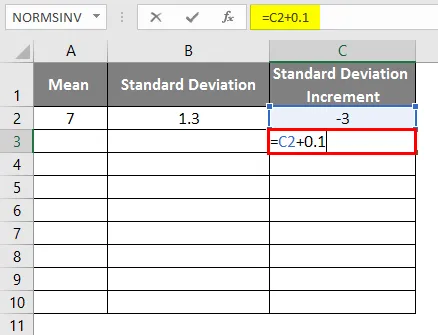
- Kaavan soveltamisen jälkeen tulos on seuraava.
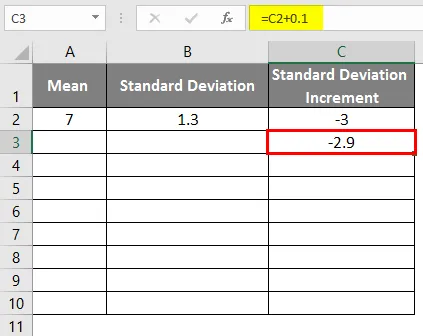
- Vedä arvoja saadaksesi lisää arvoja, kunnes saamme positiiviset arvot niin, että saamme vasemman käyrän.
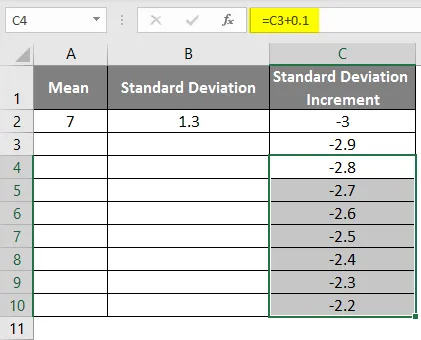
- Oikean käyrän saamiseksi meidän on käytettävä kaavaa = keskimääräinen keskipoikkeama * 3, jotta saadaan tarkat käyrät.
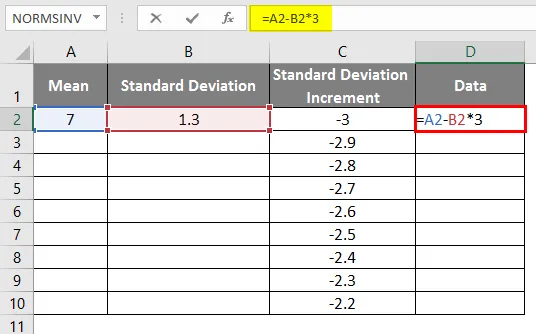
- Kaavan käytön jälkeen tulos näkyy alla.
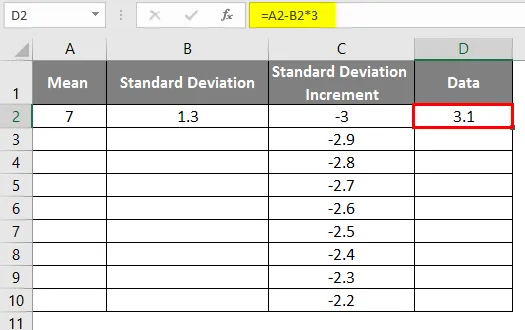
- Kuten yllä olevissa tiedoissa vakiopoikkeaman lisäyksestä vasemman käyrän saamiseksi, olemme lisänneet arvoja 0, 1
- Samaa skenaariota käytetään soveltamalla kaavaa kuin = 3, 1 + VAKIOLAIKOISUUS / 10 käyrän lisäyksen 0, 1 saamiseksi
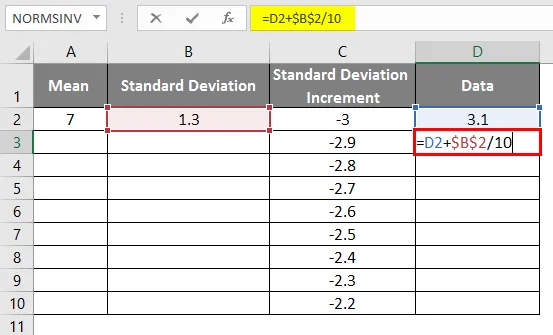
- Kaavan käytön jälkeen tulos näkyy alla.

- Vedä arvoja saadaksesi tarkan tuloksen, joka näkyy alla olevassa kuvakaappauksessa.
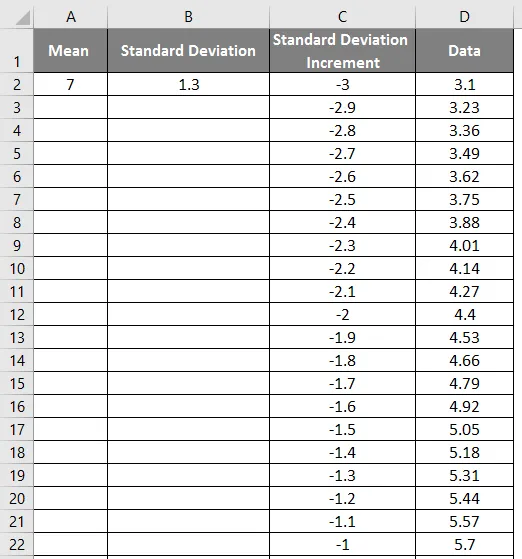
- Käytä nyt normaalia jakelufunktiota kaavalla = NORM.DIST (DATA-arvo, keskiarvo, keskihajonta, väärä).
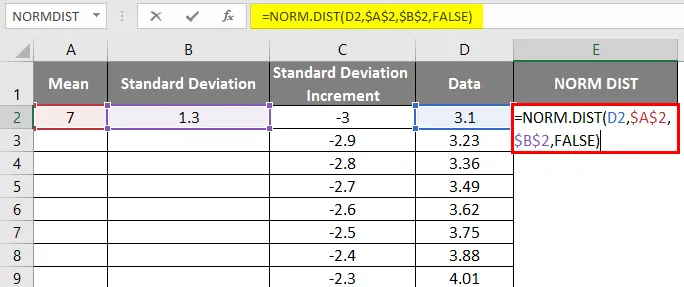
- Saadaan alla oleva tulos seuraavalla tavalla.
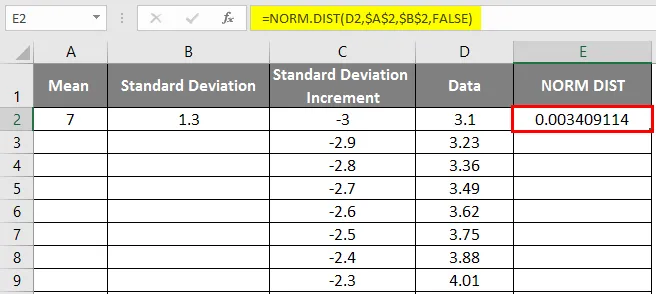
- Vedä arvoja saadaksesi tarkan tuloksen, joka on esitetty alla.
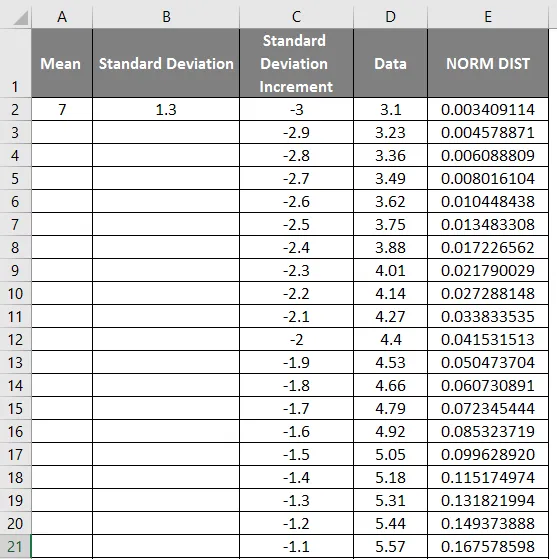
- Kuten yllä olevassa kuvakaappauksessa voidaan nähdä, olemme laskeneet NORMAL-jakauman keskiarvosta ja keskihajonnasta. Katsotaan nyt, mikä on NORMAL-jakauman käänteinen soveltamalla alla olevaa NORMSINV-arvoa.
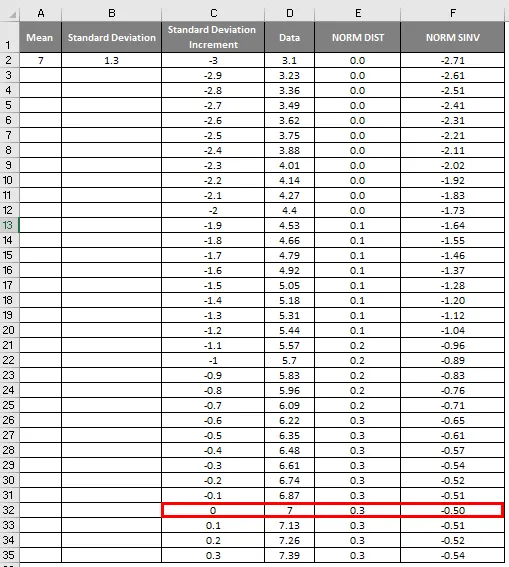
- Täällä voimme nähdä, että arvon nolla (0) vakiopoikkeama on 7.

Hajautetun kuvaajan avulla katsotaan, kuinka vasen ja oikea käyrä näkyvät.
- Valitse ensin tiedot ja Normaali-sarake.
- Siirry Lisää-välilehteen ja valitse hajautettu kaavio seuraavasti.
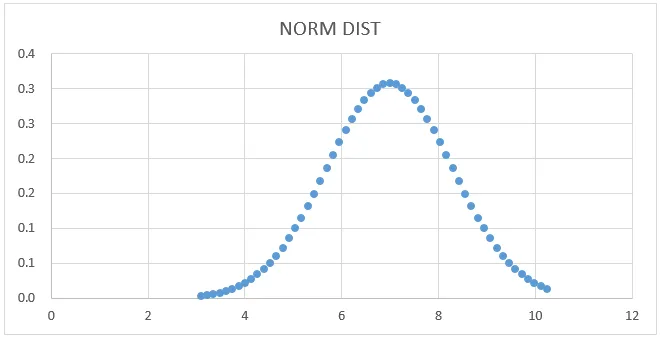
- Saadaan alla oleva käyräkaavio alla esitetyllä tavalla.
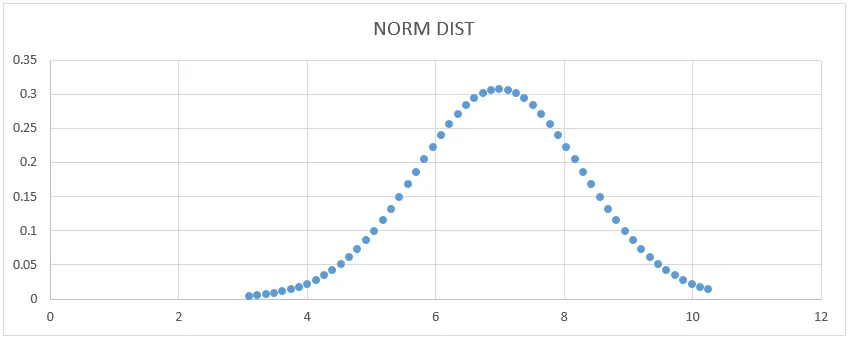
Täällä voimme nähdä, että keskiarvolla 7 on keskihajonnan muoto, jossa voimme osoittaa sen vetämällä suoran linjan esittämään sitä.
- Keskiarvo = 7
- 1 - Vakiopoikkeama ilmoittaa 68% tiedoista.
- 2 - Normaali poikkeama osoittaa 95% tiedoista.
- 3 - Normaali poikkeama osoittaa 99, 7% tiedoista.
Normaali jakaumakaavio:
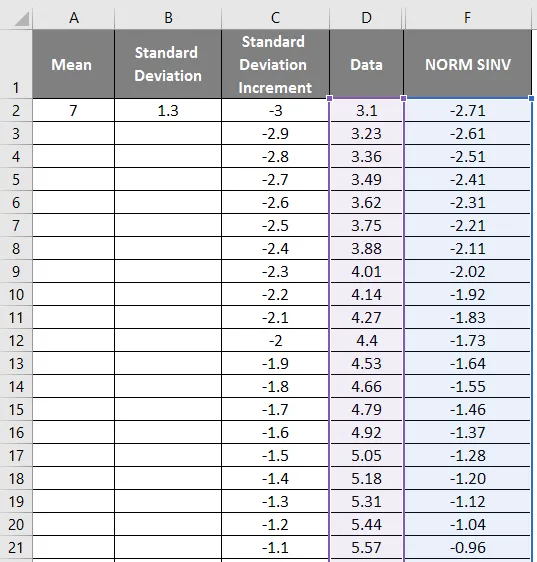
NORMSINV-kuvaaja:
Valitse nyt yllä olevasta kuvasta datasarake ja NORM SINV saadaksesi alla olevan kuvaajan seuraavasti.
- Valitse ensin tiedot ja Normaali-sarake.
- Siirry Lisää-välilehteen ja valitse hajautettu kaavio.
- Saamme alla olevan kuvaajan, joka näkyy alla olevassa kuvakaappauksessa.
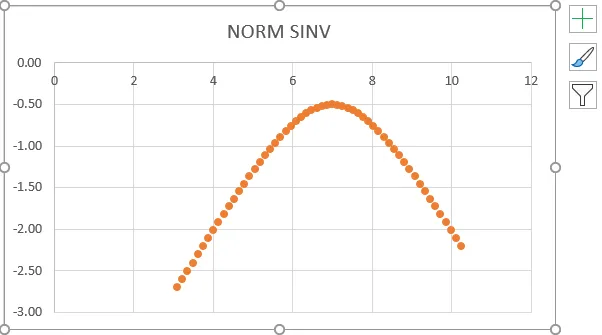
- Yllä olevasta kuvakaappauksesta voidaan nähdä, että saimme tarkan käänteisen normaalijakaumasta, joka näyttää saman arvon kuin alla.

Esimerkki 3 - Vasemman ja oikean käyrän konfigurointi
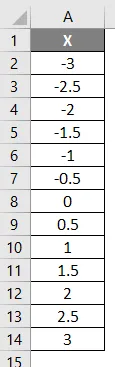
Tässä esimerkissä konfiguroimme vasen ja oikea käyrä normaalia jakelutoimintoa käyttämällä. Tarkastele alla olevia tietoja alla esitetyllä tavalla, missä x: llä on negatiiviset arvot ja se kasvaa positiivisiksi arvoiksi.
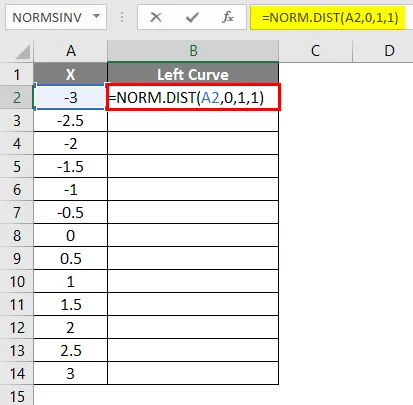
- Käytä kaavaa = NORM.DIST (A2, 0, 1, 1).
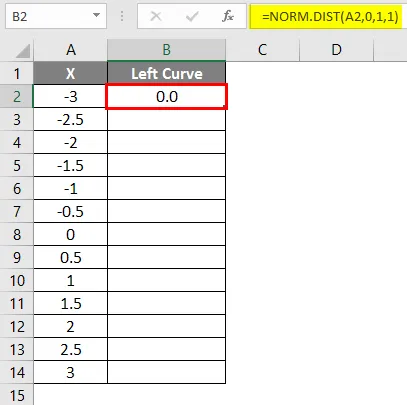
- Kaavan soveltamisen jälkeen tulos näkyy alla.
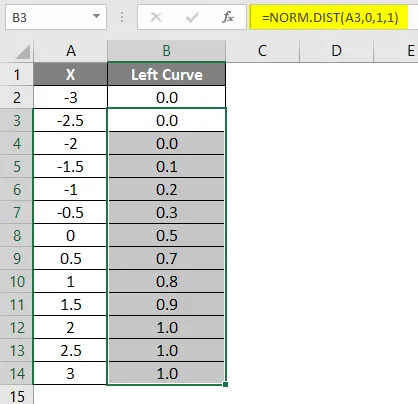
- Vedä kaava muihin soluihin.
- Käytä kaavaa = 1-B2 .
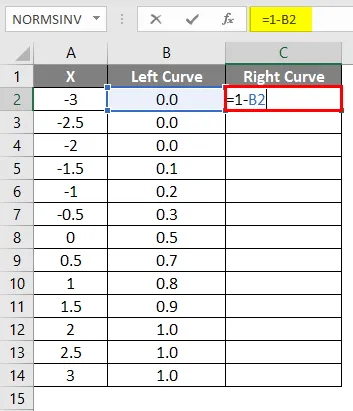
- Kaavan soveltamisen jälkeen tulos näkyy alla.
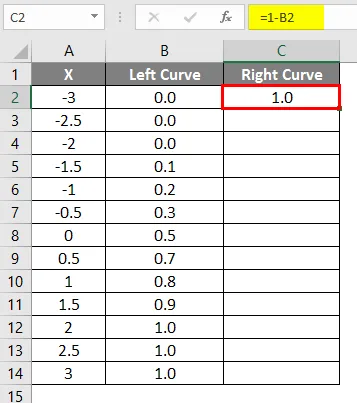
- Vedä sama kaava muihin soluihin.
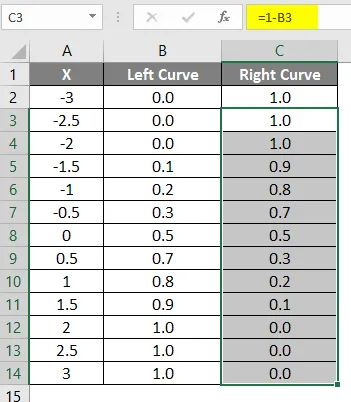
Edellä käytetyn kaavan tulos esitetään alla.
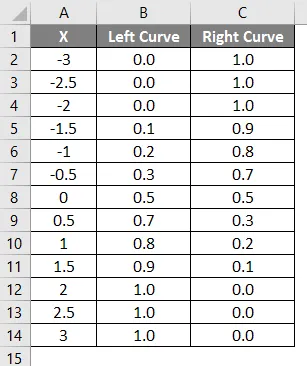
- Vasemman käyrän arvot on laskettu soveltamalla NORMAL DISTRIBUTION -kaavaa asettamalla kumulatiiviseksi arvoksi True ja NORMSINV on laskettu käyttämällä vasenta käyrää.
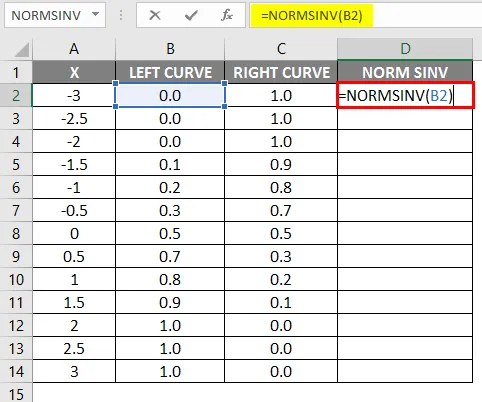
- Kaavan soveltamisen jälkeen tulos näkyy alla.
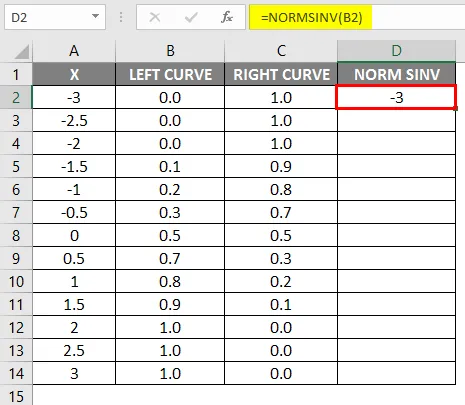
- Vedä sama kaava muihin soluihin.
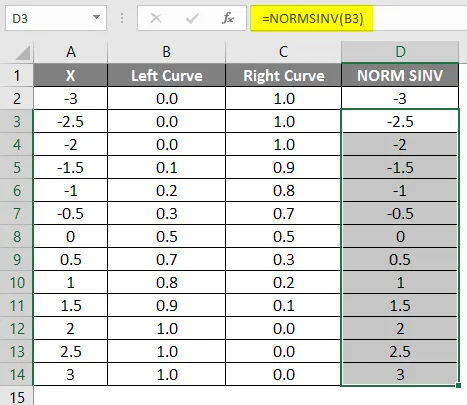
Kuten voimme nähdä, että saimme saman arvon NORMSINV: lle, mikä on vain normaalin jakauman käänteinen arvo. Samalla tavalla saadaan oikea käyräarvo laskemalla yhden vasemman käyrän arvo. Seuraavassa vaiheessa aiomme tarkistaa, kuinka saadaan x: n korkeus käyttämällä hajautettua kuvaajaa.
- Valitse vasen kovetus- ja oikea käyräsarake.
- Siirry lisää valikkoon.
- Valitse hajautettu kaavio seuraavasti.
Saamme alla olevan kuvaajan tuloksen alla esitetyllä tavalla.
NORM SINV -diagrammi:
Alla olevassa kaaviossa voimme nähdä, että NORM DISTRIBUTION -arvon vasemmalla käyrällä on tarkka vastaavuus (0, 0, 5), joka sijaitsee sen rivin keskellä, josta saadaan sama kuvaaja, jos haemme NORMDIST-arvoa.
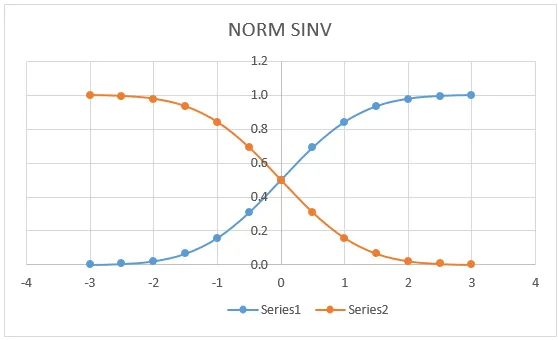
Tässä yllä olevassa kaaviossa se osoittaa erittäin selvästi, että saimme tarkan keskiarvon keskipisteessä, joka osoittaa:
- X = 0
- Vasen käyrä = 0, 5
- Oikea käyrä = 0, 5
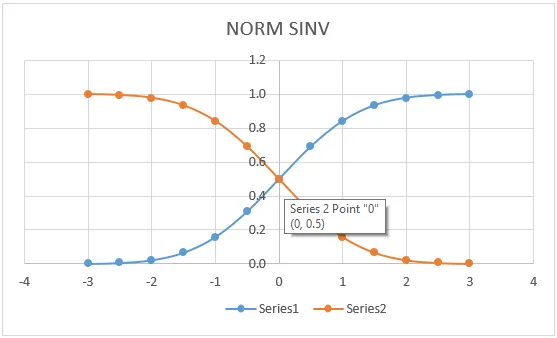
Näytimme sen nähdäksesi NORMSINV-arvot graafisessa muodossa, kuten alla on esitetty.
Muistettavat tiedot Excel NORMSINV: stä
- #arvo! Virhe tapahtuu, kun annettu argumentti ei ole numeerinen tai looginen arvo.
- Normaalijakelutoiminnossa saamme yleensä #NUM! Normaalipoikkeluargumentista johtuva virhe on pienempi tai yhtä suuri kuin nolla.
Suositellut artikkelit
Tämä on opas Excel NORMSINV -sovellukseen. Tässä keskustellaan siitä, miten NORMSINV: ää voidaan käyttää Excelissä, sekä käytännön esimerkkejä ja ladattavaa excel-mallia. Voit myös käydä läpi muiden ehdottamiemme artikkeleidemme -
- Kuinka käyttää nimikenttää Excelissä?
- Työskentely Matrixin kanssa Excelissä
- Entä jos Excel-analyysi
- NPV-kaava Excelissä