
Virhekaavan kaava (sisällysluettelo)
- Virhemarginaali
- Esimerkkejä virhekaavan marginaalista (Excel-mallilla)
- Virhemarginaali kaavan laskin
Virhemarginaali
Tilastossa lasketaan luottamusväli nähdäksesi mihin näytteen tilastotietojen arvo laskee. Arvoalue, joka on luottamusvälin sisällä näytteen tilastotietojen alapuolella ja yläpuolella, tunnetaan virhemarginaalina. Toisin sanoen, se on pohjimmiltaan virhetaso otantatilastoissa. Mitä korkeampi virhemarginaali, sitä heikompi on luottamus tuloksiin, koska poikkeama näiden tulosten suhteen on erittäin korkea. Kuten nimensä osoittaa, virhemarginaali on arvoalue todellisten tulosten ylä- ja alapuolella. Esimerkiksi, jos saamme vastauksen kyselyyn, jossa 70% ihmisistä on vastannut ”hyvällä” ja virhemarginaali on 5%, tämä tarkoittaa sitä, että yleensä 65–75% väestöstä ajattelee vastauksen olevan ”hyvä” .
Kaava virhemarginaalille -
Margin of Error = Z * S / √n
Missä:
- Z - Z pisteytys
- S - populaation keskihajonta
- n - näytteen koko
Toinen kaava virhemarginaalin laskemiseksi on:
Margin of Error = Z * √((p * (1 – p)) / n)
Missä:
- p - Näytteen osuus (onnistuneen näytteen osuus)
Nyt löytääksesi halutun z-pistemäärän, sinun on tiedettävä näytteen luottamusväli, koska Z-pistemäärä riippuu siitä. Alla oleva taulukko antaa nähdä luottamusvälin ja z-pisteet:
| Luottamusväli | Z - Pisteet |
| 80% | 1.28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Kun tiedät luottamusvälin, voit käyttää vastaavaa z-arvoa ja laskea virhemarginaalin sieltä.
Esimerkkejä virhekaavan marginaalista (Excel-mallilla)
Otetaan esimerkki ymmärtääksesi virhemarginaalin laskennan paremmin.
Voit ladata tämän virhemarginaalin täältä - virhemarginaalinVirhekaavan marginaali - esimerkki # 1
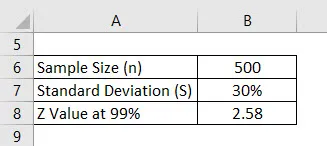
Oletetaan, että teemme kyselyn nähdäksemme, millainen arvosana yliopisto-opiskelijoille on. Olemme valinneet satunnaisesti 500 opiskelijaa ja kysyneet arvosanansa. Tämän keskiarvo on 2, 4 neljästä ja keskihajonta on esimerkiksi 30%. Oletetaan, että luottamusväli on 99%. Laske virhe.
Ratkaisu:
Virhemarginaali lasketaan alla olevan kaavan avulla
Virhemarginaali = Z * S / √n
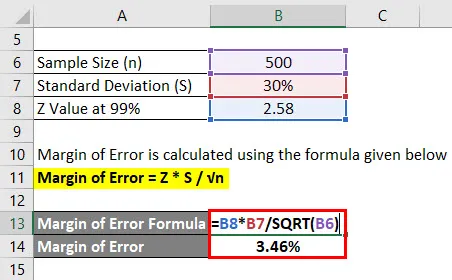
- Virhemarginaali = 2, 58 * 30% / √ (500)
- Virhemarginaali = 3, 46%
Tämä tarkoittaa, että luotettavuudella 99% opiskelijoiden keskimääräinen arvosana on 2, 4 plus tai miinus 3, 46%.
Virhekaavan marginaali - esimerkki 2
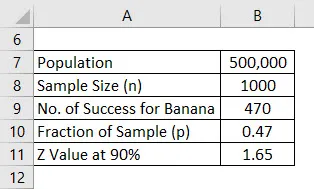
Sanotaan, että lanseerat markkinoille uuden terveystuotteen, mutta olet hämmentynyt siitä, mikä maku ihmisille tulee. Olet sekoittunut banaanin maun ja vanilja-aromin välillä ja olet päättänyt suorittaa tutkimuksen. Väestösi sillä on 500 000, mikä on kohdemarkkinaasi, ja päätitte kysyä 1000 ihmisen mielipidettä ja se tulee otokseen. Oletetaan, että luottamusväli on 90%. Laske virhe.
Ratkaisu:
Kun kysely on tehty, tiesit, että 470 ihmistä piti banaanin mausta ja 530 on pyytänyt vaniljamakua.
Virhemarginaali lasketaan alla olevan kaavan avulla
Virhemarginaali = Z * √ ((p * (1 - p)) / n)
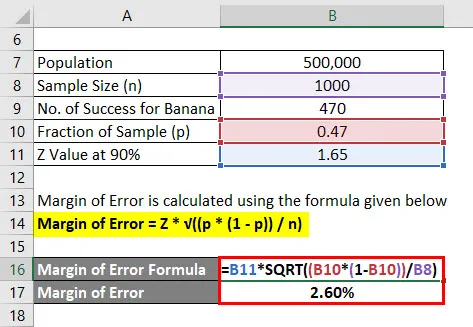
- Virhemarginaali = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Virhemarginaali = 2, 60%
Joten voimme sanoa, että 90 prosentilla varmuudella 47% kaikista ihmisistä piti banaanin makua plus tai miinus 2, 60%.
Selitys
Kuten edellä käsiteltiin, virhemarginaali auttaa meitä ymmärtämään, onko kyselysi otoskoko sopiva vai ei. Jos marginaalivirhe on liian suuri, voi olla, että otoskoko on liian pieni ja meidän on lisättävä sitä niin, että otoksen tulokset vastaavat paremmin populaatiotuloksia.
Joissakin tilanteissa virhemarginaalista ei ole paljon hyötyä eikä se auta meitä virheen jäljittämisessä:
- Jos kyselyn kysymyksiä ei ole suunniteltu eivätkä ne auta vaadittavan vastauksen saamisessa
- Jos kyselyyn reagoivilla ihmisillä on jonkin verran harhoja tuotteeseen, jota varten tutkimusta tehdään, niin myös tulos ei ole kovin tarkka
- Jos itse valittu otos edustaa väestöä oikein, niin myös silloin tulokset ovat kaukana.
Lisäksi yksi iso oletus on, että väestö on normaalisti jakautunut. Joten jos otoksen koko on liian pieni ja populaation jakauma ei ole normaalia, z-pistettä ei voida laskea eikä emme löydä virherajaa.
Virhekaavan relevanssi ja käyttötavat
Aina kun etsimme näytteitä tietyn asiaankuuluvan vastauksen löytämiseksi joukkojoukkoon, on jonkin verran epävarmuutta ja mahdollisuuksia, että tulos saattaa poiketa todellisesta tuloksesta. Virhemarginaali kertoo meille, että mikä on poikkeama, on näytteen lähtö. Meidän on minimoitava virhemarginaali, jotta näytteemme tulokset kuvaavat todellista väestötietojen tarinaa. Joten alenna virhettä, sitä paremmat ovat tulokset. Virhemarginaali täydentää ja täydentää meillä olevia tilastotietoja. Esimerkiksi, jos tutkimuksen mukaan 48% ihmisistä mieluummin viettää aikaa kotona viikonloppuna, emme voi olla niin tarkkoja, ja tiedoista puuttuu joitain elementtejä. Kun otimme käyttöön virhemarginaalin, esimerkiksi 5%, tulosta tulkitaan siten, että 43–53% ihmisistä piti ajatuksesta olla kotona viikonloppuna, mikä on täysin järkevää.
Virhemarginaali kaavan laskin
Voit käyttää seuraavaa virhemarginaalia
| Z | |
| S | |
| √n | |
| Virhemarginaali | |
| Virhemarginaali | = |
|
|
Suositellut artikkelit
Tämä on opas virhemarginaalin kaavaan. Tässä keskustellaan siitä, kuinka virhemarginaali voidaan laskea yhdessä käytännön esimerkkien kanssa. Tarjoamme myös virhemarginaalilaskurin ladattavalla excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Opas suoraviivaiseen poistokaavaan
- Esimerkkejä kaksinkertaisen ajan kaavasta
- Kuinka laskea poistot?
- Kaava keskusrajalauseelle
- Altman Z-pistemäärä | Määritelmä | esimerkit
- Poistokaava | Esimerkkejä Excel-mallilla