
Aritmeettinen keskiarvokaava (sisällysluettelo)
- Kaava
- esimerkit
- Laskin
Mikä on aritmeettinen keskiarvokaava?
Termi ”aritmeettinen keskiarvo” viittaa periaatteessa kahden tai useamman numeron matemaattiseen keskiarvoon. Aritmeettisen keskiarvon laskemismenetelmä voi kuitenkin vaihdella tietojoukon kunkin muuttujan taajuuden perusteella - yksinkertainen keskiarvo (yhtä painotettu) tai painotettu keskiarvo. Tasapainotettujen muuttujien aritmeettisen keskiarvon kaava voidaan johtaa laskemalla yhteen kaikki tietojoukon muuttujat ja jakamalla sitten tulos muuttujien lukumäärällä. Matemaattisesti se esitetään
Arithmetic Mean = (x 1 + x 2 + …. + x n ) / n
tai
Arithmetic Mean =∑ x i / n
Missä,
- x i = i. muuttuja
- n = tietojoukon muuttujien lukumäärä
Epätasaisesti painotettujen muuttujien tapauksessa aritmeettisen keskiarvon kaava voidaan johtaa laskemalla yhteen kunkin muuttujan tulokset ja sen taajuus, ja sitten tulos jaetaan taajuuksien summalla. Matemaattisesti se esitetään
Arithmetic Mean = (f 1 *x 1 +f 2 *x 2 + …. + f n *x n ) / (f 1 + f 2 + ….. + f n )
tai
Arithmetic Mean = ∑ (f i * x i ) / f i
Missä
- x i = i. muuttuja
- f i = i: nnen muuttujan taajuus
Esimerkkejä aritmeettisesta keskimääräisestä kaavasta (Excel-mallilla)
Otetaan esimerkki ymmärtää aritmeettisen keskiarvon laskenta paremmin.
Voit ladata tämän aritmeettisen keskiarvon Formula Excel -mallin tästä - Aritmeettinen keskiarvo Formula Excel -malliAritmeettinen keskiarvokaava - esimerkki # 1
Otetaanpa esimerkki lepakoitsijasta, joka teki seuraavan juoksun viimeisen kymmenen vuoronsa aikana viimeisen vuoden aikana: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Laske batsmanin keskiarvo viimeisimmästä 10 sisävuoro.
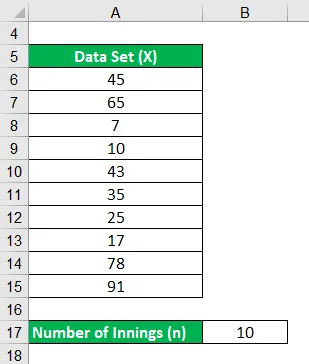
Ratkaisu:
Aritmeettinen keskiarvo lasketaan alla olevan kaavan avulla
Aritmeettinen keskiarvo = ∑ x i / n
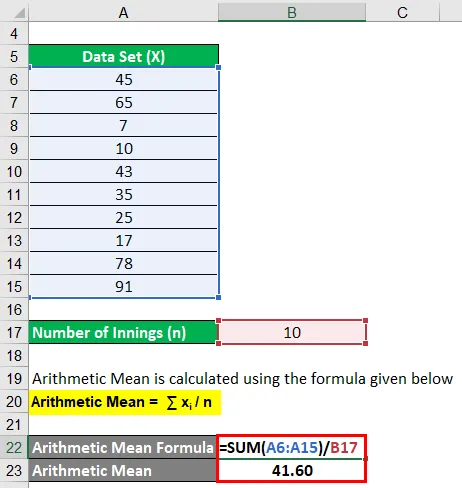
- Aritmeettinen keskiarvo = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Aritmeettinen keskiarvo = 41, 60
Siksi lyöjän keskiverto pysyi 41, 60 juoksua innota kohti viimeisen 10 inningin aikana.
Aritmeettinen keskiarvokaava - esimerkki 2
Otetaanpa esimerkki luokasta, jossa on 45 oppilasta. Äskettäin suoritettiin viikoittainen luonnontieteellinen testi, jossa opiskelijat arvioitiin asteikolla 1-10. Laske seuraavien tietojen perusteella testin keskiarvot.
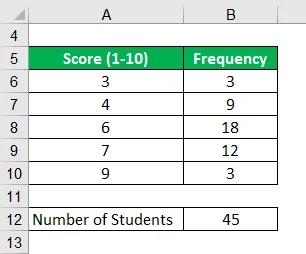
Ratkaisu:
Aritmeettinen keskiarvo lasketaan alla olevan kaavan avulla
Aritmeettinen keskiarvo = ∑ (f i * x i ) / f i
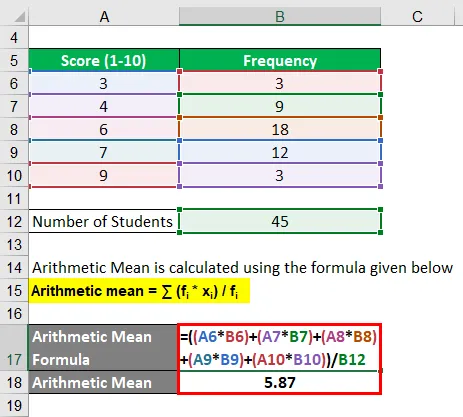
- Aritmeettinen keskiarvo = ((3 * 3) + (4 * 9) + (6 * 18) + (7 * 12) + (9 * 3)) / 45
- Aritmeettinen keskiarvo = 264/45
- Aritmeettinen keskiarvo = 5, 87
Siksi luokan keskimääräinen pistemäärä tiedetestissä oli 5, 87.
Aritmeettinen keskiarvokaava - esimerkki 3
Otetaan esimerkki kahdesta tietojoukosta, joissa on kaksi erilaista aritmeettista keskiarvoa. Ensimmäisessä tietojoukossa on 10 muuttujaa, joiden keskiarvo on 45, kun taas toisessa tietojoukossa on 7 muuttujaa ja keskiarvo on 42. Määritä kahden tietojoukon yhdistelmän aritmeettinen keskiarvo.
Ratkaisu:
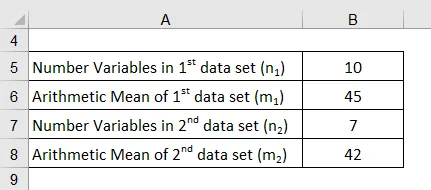
Yhdistetyn tietojoukon aritmeettinen keskiarvo lasketaan alla olevan kaavan avulla
Aritmeettinen keskiarvo = ((m 1 * n 1 ) + (m 2 * n 2 )) / (n 1 + n 2 )
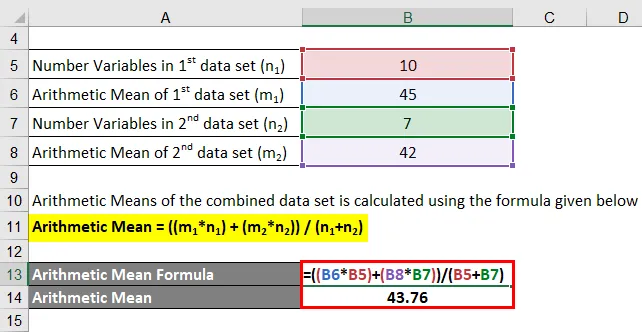
- Aritmeettinen keskiarvo = (45 * 10 + 42 * 7) / (10 + 7)
- Aritmeettinen keskiarvo = 43, 76
Siksi yhdistetyn tietojoukon aritmeettinen keskiarvo on 43, 76.
Selitys
Aritmeettisen keskiarvon kaava voidaan laskea käyttämällä seuraavia vaiheita:
Vaihe 1: Ensin kerätään ja lajitella muuttujat, joiden aritmeettinen keskiarvo on laskettava. Muuttujat on merkitty x i: llä .
Vaihe 2: Seuraavaksi määritetään muuttujien lukumäärä tietojoukossa, ja se merkitään n: llä yhtä painotettujen muuttujien tapauksessa. Muussa tapauksessa selvitä kunkin muuttujan taajuus ja ne merkitään f i: llä, ja muuttujien lukumäärä on taajuuksien summaus.
Vaihe 3: Lopuksi voidaan laskea yhtälölle painotettujen muuttujien aritmeettisen keskiarvon kaava lisäämällä kaikki muuttujat ja sitten tulos jaetaan tietojoukon muuttujien lukumäärällä, kuten alla on esitetty.
Aritmeettinen keskiarvo = ∑ x i / n
Kuitenkin painotetun keskiarvon tapauksessa aritmeettisen keskiarvon kaava voidaan johtaa laskemalla yhteen kunkin muuttujan tulokset ja sen taajuus, ja sitten tulos jaetaan taajuuksien summalla, kuten alla on esitetty.
Aritmeettinen keskiarvo = ∑ f i * x i / f i
Aritmeettisen keskiarvokaavan relevanssi ja käyttö
Aritmeettisen keskiarvon käsite on hyvin yksinkertainen ja yksinkertainen. Mutta se on silti erittäin tärkeä, koska sitä käytetään usein tilastollisena indikaattorina arvioimaan tietojoukon keskimääräinen tulos. Itse asiassa se antaa mahdollisuuden arvioida, mitkä muuttujat ovat parempia tai pienempiä kuin ryhmän keskiarvo. Sitä käytetään myös mittana edustamaan keskimääräistä arvoa koko datasarjassa. Lisäksi aritmeettista keskiarvoa käytetään tapauksissa, joissa geometrinen keskiarvo tai harmoninen keskiarvo ovat vähemmän hyödyllisiä, kuten keskimääräinen aste, paino jne.
Aritmeettinen keskiarvokaavalaskin
Voit käyttää seuraavaa aritmeettista keskiarvolaskuria
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Aritmeettinen keskiarvo | |
| Aritmeettinen keskiarvo | = |
|
|
Suositellut artikkelit
Tämä on opas aritmeettiseen keskiarvokaavaan. Tässä keskustellaan kuinka laskea aritmeettinen keskiarvo yhdessä käytännön esimerkkien kanssa. Tarjoamme myös aritmeettisen keskiarvon laskurin ladattavalla excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Kuinka laskea harmoninen keskiarvo?
- Opas väestön keskimääräiseen kaavaan
- Keskiarvon laskeminen kaavaa käyttäen
- Esimerkkejä liikevaihtokaavasta