
Yleiskatsaus taloustieteestä
Talous on tiede, joka tutkii ihmisen käyttäytymistä eri tilanteissa ja johtaa erilaisia päätelmiä, joista on hyötyä yritykselle. Taloustiedettä pidetään myös valinnan tekemisen tieteenä, joka auttaa ihmistä valitsemaan erilaisia tekijöitä vaatimuksensa perusteella. Kaikkien taloudellisten lauseiden tai sääntöjen perusoletus on, että ihminen on rationaalinen ja ajattelee sivistyneessä yhteiskunnassa.
Taloudessa on erilainen käsite, mutta olemme yrittäneet kuvata alla mainittua tärkeintä taloustieteen käsitettä.
Esimerkkejä taloudesta
Käyttämällä joitain yleisiä tai reaalimaailman esimerkkejä, taloustiede voidaan ymmärtää paremmin: -
Taloustiede Esimerkki 1 - Kuluttajaylijäämä
Kuluttajaylijäämä on kuluttajan kyky maksaa hinnasta mistä tahansa hyödykkeestä verrattuna markkinoilla vallitsevaan todelliseen hintaan.
Kuten prof. Alfred Marshall,
"Ylijäämä, jonka henkilö on valmis maksamaan sen sijaan, että pysyisi ilman asiaa, sen verran, mitä hän tosiasiallisesti maksaa, on hyödyllisyysylijäämän mittaaminen - joka tunnetaan kuluttajan ylijäämänä."
- Kuluttajan ylijäämä = Hinta valmis maksamaan (-) Hinta tosiasiallisesti maksettu
- Kuluttajan ylijäämä = kokonaiskäyttö - (P * Q)
- Kuluttajan ylijäämä = hyödyllisyys yhteensä - kulut yhteensä.
Ymmärretään tämä käsite esimerkin avulla:
Kuva
On tuote A, jonka marginaalinen hyöty ja yksikköhinnat ovat seuraavat:
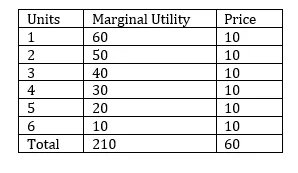
Laske tämän perusteella kuluttajan ylijäämä ja piirtä sama käyrälle, jolla on asianmukainen kuvaus.
Ratkaisu:
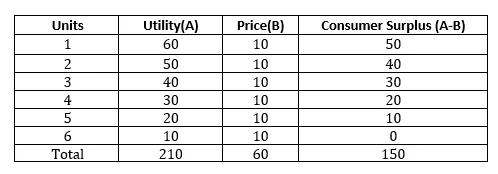
Taulukosta käy selvästi ilmi, että kuuden yksikön kuluttaja oli valmis maksamaan 210, mutta hänen oli maksettava 60. Siksi kuluttajan ylijäämä = 210 - 60 = 150
Kuluttajaylijäämäkäyrä
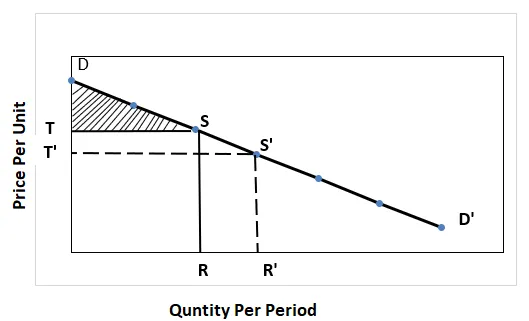
Kuvassa meillä on varjostettu alue, joka osoittaa kuluttajan ylijäämän.
Kuluttajan ylijäämän hyödyllisyys
(i) Se auttaa tekemään taloudellisia vertailuja ihmisten hyvinvoinnista kahden paikan tai maan välillä.
(ii) Käsite on hyödyllinen ymmärrettäessä syrjivän monopolin hinnoittelupolitiikkaa ja pyyhkimällä ylijäämä erilaisella syrjinnällä.
(iii) Se auttaa hyödykkeen veron taloudellisten vaikutusten arvioinnissa.
(iv) Se auttaa mittaamaan kansainvälisen kaupan hyötyjä.
Taloustiede Esimerkki 2 - Lyhytaikaiset kustannukset
Lyhyellä aikavälillä monet tuotannontekijät eivät muutu, ja siksi ne pysyvät ennallaan. Kustannuksia, jotka yritykselle aiheutuu tuotannosta riippumatta, kutsutaan kiinteiksi kokonaiskustannuksiksi (TFC). Kiinteät kustannukset pysyvät ennallaan eikä muutu millään tuotoksen tasolla. Lyhyellä aikavälillä vain lähtöä voidaan hallita, joten kustannuksia, jotka muutokset perustuvat tuotokseen, kutsutaan muuttuviksi kustannuksiksi. (TVC). Lisäämällä kiinteät ja muuttuvat kustannukset, saamme yrityksen kokonaiskustannukset (TC)
Kaava
- TC = TVC + TFC
- SAC = TC / q
- AVC = TVC / q
- AFC = TFC / q
- SMC = kokonaiskustannusten muutos / tuotannon muutos = ΔTC / q
Tuotannon tuotannon lisäämiseksi yrityksen on käytettävä enemmän muuttuvia tuotantopanoksia. Seurauksena muuttuvien kokonaiskustannusten ja kokonaiskustannusten nousu. Näin ollen tuotannon kasvaessa muuttuvat kustannukset kasvavat, mutta kiinteät kustannukset pysyvät ennallaan.
Kuva:
ABC Ltd aikoo perustaa tehtaan. Se aikoo valmistaa hyödykkeen. Tulokseen perustuva yksityiskohtainen kustannusohjelma on seuraava:
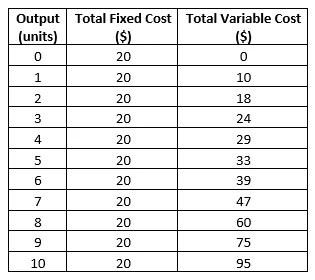
Laske keskimääräiset kiinteät kustannukset (AFC), keskimääräiset muuttuvat kustannukset (AVC), lyhyen aikavälin keskimääräiset kustannukset (SAC) ja lyhyen aikavälin rajakustannukset (SMC)
Ratkaisu :
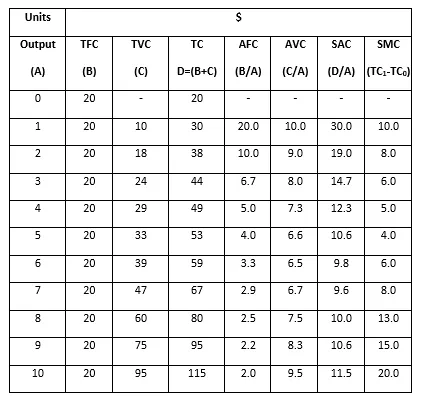
Yllä oleva laskelma perustuu seuraaviin kaavoihin:
- Kokonaiskustannukset = Kiinteät kokonaiskustannukset + muuttuvat kokonaiskustannukset
- Keskimääräiset kiinteät kustannukset = Kiinteät kokonaiskustannukset / tuotos
- Keskimääräinen muuttuva hinta = Muuttuva kokonaiskustannus / tuotos
- Lyhyen aikavälin keskihinta = kokonaiskustannukset / tuotos
- Lyhytaikaiset rajakustannukset = Kokonaiskustannukset tuotosta Q 1 - Kokonaiskustannukset tuotosta Q 0
Kaavio:
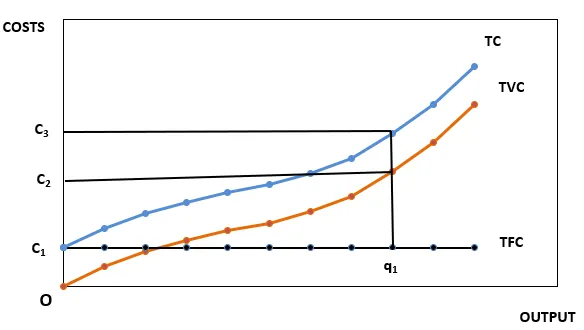
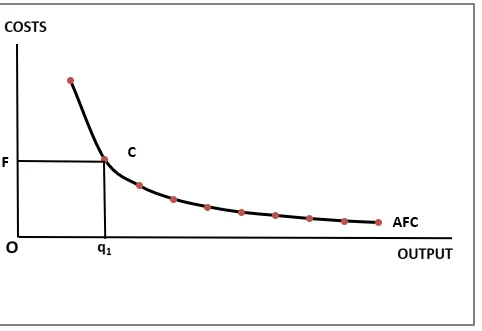
Yllä olevassa kaaviossa voimme havaita, että:
- Kiinteät kustannukset pysyvät samoina tuotannosta riippumatta
- Muuttuvat kustannukset nousevat alennetulla nopeudella
- Kokonaiskustannukset alkavat kiinteillä kustannuksilla ja kasvavat samanaikaisesti muuttuvien kustannusten kanssa
- AFC-käyrä on itse asiassa suorakaiteen muotoinen hyperbooli. AFC on TFC: n ja q: n välinen suhde. TFC on vakio. Siksi, kun q kasvaa, AFC laskee. Kun lähtö on hyvin lähellä nollaa, AFC on mielivaltaisesti suuri, ja kun lähtö siirtyy kohti ääretöntä, AFC siirtyy kohti nollaa.
Päättely:
- Rajakustannukset ovat TVC: n lisäys, joka johtuu yhden ylimääräisen tuotantoyksikön tuotannon lisääntymisestä
- Minkä tahansa tuotoksen osalta rajakustannusten summa siihen tasoon saakka antaa meille muuttuvien kokonaiskustannusten tällä tasolla.
- Keskimääräiset muuttuvat kustannukset jollain tuotantotasolla ovat siis kaikkien rajakustannusten keskiarvo siihen asti
Taloustiede Esimerkki 3 - Marginaalista hyötyä vähentävä laki
Kaikkien asiakkaiden päätavoitteena on saavuttaa maksimaalinen tyytyväisyys kaikista omistamistaan hyödykkeistä. Hyödyllisyys tarkoittaa hyötyä, joka tuotteesta voidaan saada.
Termejä, joita käytetään pääasiassa tässä, laki on kokonaishyödyllisyys ja rajahyöty. Kokonaishyödyllisyydellä tarkoitetaan kuluttajan käyttämistä hyödykkeistä johdettua hyödyllisyyttä. Marginaalisella hyödyllisyydellä tarkoitetaan lisähyödykkeen kulutuksesta saatua hyödyllisyyttä.
Laki:
- ”Lisätyytyväisyys, jota ihminen ajaa tietyn hyödykkeen kulutuksen kasvun myötä, vähenee jokaisella hyödykkeen kasvulla, joka hänellä jo on. ”
Kaava
- Marginaalinen hyöty = Hyödyllisyys Q2: sta - Q1: stä
- Siten kokonaishyöty = kaikkien marginaalisten hyötyjen summa
Kuva:
Ymmärtäkäämme mainittu laki esimerkillä:
Alex on suklaafani. Kuluttamalla yhden suklaan, hän saa hyödyksi 30 Utilia (tyytyvyyden mitta). Toisen suklaan kulutuksella hän saa tyytyväisyytensä 50 utiliaan, ja seuraava tyytyväisyys annetaan alla olevassa taulukossa:
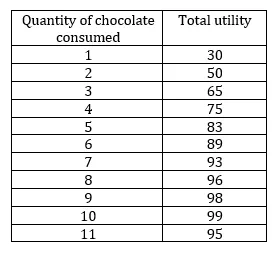
Laske yllä olevasta taulukosta marginaalinen hyöty.
Ratkaisu :
Marginaalinen hyöty = Kokonaiskäyttö Q2: lla - Kokonaiskäyttö Q1: llä
Marginaalinen hyödyllisyys johdetaan siten seuraavasta taulukosta:
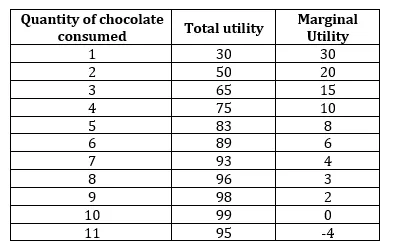
Voimme nähdä, että kulutuksen kasvaessa kokonaishyödyllisyys kasvaa; sitä kuitenkin kasvatetaan laskussa. Tämä on selvästi nähtävissä hyödyllisyyden raja-arvoissa, jotka vähenevät jatkuvasti ja jopa muuttuvat negatiivisiksi, koska yhden ajankohdan ylittävän kulutuksen jälkeen se voi johtaa sairauteen. Siksi Alexin on lopetettava kulutus, ja hänen hyödyllisyytensä suklaasta vähentää edelleen.
Sama käy ilmi alla olevasta kaaviosta:
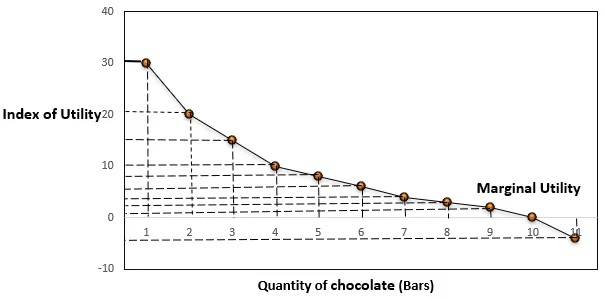
Päättely:
- Kun kokonaiskäyttöaste nousee, marginaalinen hyöty pienenee.
- Kun kokonaiskäyttö on maksimi, marginaalinen hyödyllisyys on nolla.
- Kun kokonaiskäyttöaste laskee, rajahyöty on negatiivinen.
Tämä laki auttaa meitä ymmärtämään, kuinka kuluttajat saavuttavat tasapainon millä tahansa hyödykkeellä ja miten heidän makuunsa ja mieltymyksensä vaikuttavat. Marginaalinen hyötykäyrä on laskeva, mikä osoittaa, että kuluttaja jatkaa tavaran ostamista, kunnes hyödykkeen rajahyödyllisyys tulee yhtä suureksi kuin markkinahinta. Täällä hänen tyytyväisyys on suurin.
Taloustiede Esimerkki 4 - Kysyntälaki
Kysyntälaki on yksi talousteorian tärkeimmistä laeista
Tässä laissa todetaan, että
Muut asiat pysyvät staattisina. Hintojen alentuessa siitä vaadittu määrä kasvaa ja hyödykkeen hinnan noustessa siitä vaadittu määrä vähenee. Siten vaaditun hinnan ja määrän välillä on päinvastainen suhde, muut asiat ovat staattisia.
Vaatimuksella tarkoitetaan niiden tavaroiden tai palveluiden lukumäärää, joita kuluttajat ovat halukkaita ostamaan tietyn hinta- ja ajankohdan.
Tämä voidaan ymmärtää kysyntäaikataulun ja kysyntäkäyrän avulla:
Otetaan esimerkki hyödykkeestä X, jolla on erilaiset hinta- ja markkinoisarjat, kuten alla on esitetty:
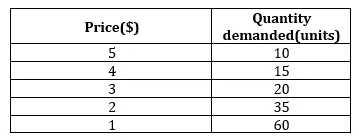
Kun hyödykkeen hinta on 5 dollaria, tuotteen kysyntä on 10 yksikköä, koska hinta laskee 4 dollariin, siellä on kysyntää 15 yksikköä, samoin, alennuksella edelleen 1 dollariin saakka, hyödykkeen kysyntä saavuttaa asti 60 yksikköä. Tämä osoittaa käänteisen suhteen hyödykkeen hinnan ja hyödykkeeltä vaaditun määrän välillä.
Piirretään yllä olevat tiedot kysyntäkäyrään,
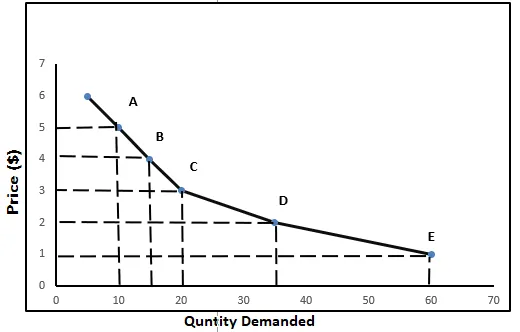
Y-akselilla olemme piirtäneet hinnan, ja X-akselilla olemme piirtäneet vaaditun määrän. Olemme kartoittaneet kaikki hinnat hyödykkeen kysynnällä pisteissä A, B, C, D ja E. Sitten olemme piirtäneet käyrän, joka kulkee kaikkien pisteiden läpi, tätä käyrää kutsutaan kysyntäkäyräksi.
Päättely:
- Ihmiset ostavat enemmän määrää halvemmalla, koska haluavat tasapainottaa hyödykkeen marginaalista hyötyä ja sen hintaa. Tätä kutsutaan marginaalisen hyödyllisyyden vähentämislakiksi
- Kun hyödykkeen hinta laskee, siitä tulee suhteellisen halvempaa kuin muihin hyödykkeisiin. Se pakottaa kuluttajat korvaamaan hyödykkeen, jonka hinta on laskenut muiden hyödykkeiden osalta, josta on tullut suhteellisen kallista. Tätä kutsutaan korvaavaksi vaikutukseksi
- Kun tuotteen hinta laskee, sama kuluttaja voi ostaa enemmän hyödykkeitä vähemmän rahalla. Toisin sanoen hintojen laskiessa kuluttajan ostovoima kasvaa, toisin sanoen reaalitulot kasvavat. Tätä kutsutaan tulovaikutukseksi.
- Hinnan alentuessa yhä useammat kuluttajat alkavat ostaa niitä, koska aiemmin kuluttajilla, joilla ei ole varaa ostaa sitä, on nyt varaa siihen.
- Harvoilla hyödykkeillä on monenlainen käyttö. Jos hinta laskee, ihmiset alkavat käyttää samaa useisiin tarkoituksiin ja yrittävät tyydyttää hyödyllisyytensä samalla hyödykkeellä.
johtopäätös
Siten taloustiede auttaa ymmärtämään, että ihmisen taipumus on erilainen liiketoiminnan tilanteessa. Se auttaa analysoimaan ihmisen käyttäytymistä heidän tarpeensa, maun, mieltymysten jne. Perusteella. Lisäksi se auttaa arvioimaan kuluttajien käyttäytymistä perustuen teollisuussykliin sekä hyödykkeiden kysyntään ja tarjontaan.
Suositellut artikkelit
Tämä on opas taloustieteelliseen esimerkkiin. Tässä keskustellaan taloustieteellisestä esimerkistä kaavion ja yksityiskohtaisen selityksen kanssa. Voit myös käydä läpi muiden ehdotettujen artikkeleidemme saadaksesi lisätietoja -
- Asteikon edut Esimerkki
- Esimerkkejä monopolistisesta kilpailusta
- Tosielämän esimerkkejä johdannaisista
- Kilpailuedun esimerkki
- Marginaalietukaava | Laskin esimerkein