Excel-lineaarinen interpolointi (sisällysluettelo)
- Mikä on interpolointi?
- Interpolointi Excel-ennustetoiminnon kanssa
- Esimerkkejä lineaarisesta interpoloinnista Excelissä
Mikä on interpolointi?
Matematiikan maailmassa interpolointi on menetelmä uusien tietopisteiden luomiseksi tunnettujen tietopisteiden avulla. Interpolointi estimoi arvon olemassa olevien käytettävissä olevien data-arvojen perusteella, jotka ovat relatoitavissa.
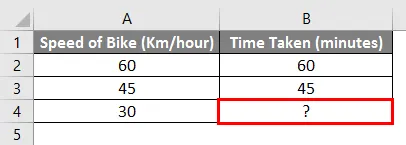
Esimerkiksi - Jos ajamme pyörällä nopeudella 60 km / h ja saavutamme tietyn määränpään 1 tunnissa ja jos ajamme nopeudella 45 km / h ja saavutamme tiettyyn määränpäähän 45 minuutissa. Joten kuinka paljon aikaa määränpäähän saaminen vie, jos ajamme nopeudella 30 km / h.
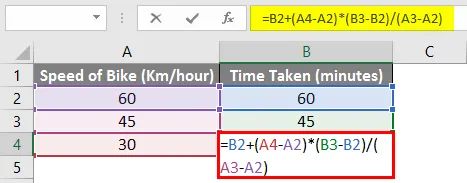
Yksinkertaisen matematiikan avulla voimme laskea puuttuvat arvot yllä olevasta esimerkistä. Meidän on lisättävä seuraava kaava soluun B4.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
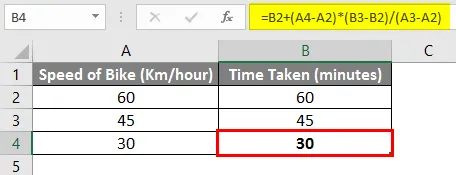
Joten yllä olevan kaavan perusteella voidaan sanoa, että määränpään saavuttaminen vie 30 minuuttia, jos ajamme nopeudella 30 km / h.
Yritetään murtaa yllä oleva kaava ja ymmärtää kaava yksityiskohtaisesti.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Yllä olevassa esimerkissä kaavan viimeinen osa, joka on korostettu punaisella, laskee kuinka paljon aikaa muuttuu aina, kun pyörän nopeus muuttuu yhdellä. Esimerkissämme kulunut aika muuttuu yhdellä minuutilla, kun pyörän nopeus muuttuu 1 km /tunnin.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Toinen osa (yllä sinisellä) laskee kuinka kaukana pyörämme nopeus on ensimmäisestä pyörän nopeudesta, kerrotaan sitten yllä lasketulla arvolla. Esimerkkimme perusteella se on 30 (solu A4) miinus 60 (solu A2), jonka tulos kerrotaan sitten yhdellä (joka vastaa -30).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Lopuksi kaavan ensimmäinen osa (yllä ruskealla); lisäämme pyörän nopeuden ensimmäisen arvon. Esimerkissämme tämä antaa lopputuloksen 60 + (-30) * (1) = 30 minuuttia. Koulussa käyimme alla olevaa kaavaa laskeaksesi Y: n puuttuvan arvon.
Y = Y1 + (X-X1) * (Y2-Y1) / (X2 - X1)
Tämä on esimerkki siitä, kuinka puuttuvat arvot voidaan laskea manuaalisen kaavan avulla interpoloinnin ymmärtämiseksi.
Excelissä on sisäänrakennettu toiminto, joka suorittaa samanlaisen laskelman kuin yllä, ja se tunnetaan ennustetoimintona. Nyt opimme tämän toiminnon yksityiskohtaisesti nyt.
Interpolointi ennustefunktioon Excelissä
Ennuste on MS Excel -sovelluksessa oleva laskentataulukkopohja ja se käyttää lineaarista regressiota puuttuvan arvon selvittämiseen. Ennuste, kuten nimensä osoittaa, sitä käytetään ennustamaan datapisteen tulevaisuuden arvo, mutta sitä voidaan käyttää myös arvon interpolointiin. Periaatteessa sitä käytetään tulevaisuuden arvon laskemiseen tietyn tietojoukon olemassa olevien arvojen perusteella.
Ennustefunktion syntaksi

Ennustetoiminnan perusteet:
- x - Se on datapiste, josta haluamme tietää tuloksena olevan arvon.
- Known_y's - Solualue, joka sisältää arvot Y.
- Tunnetut_x - solualue, joka sisältää arvot X.
Nyt kun tarkastellaan samaa yllä olevaa esimerkkiä, yritetään käyttää ennustetoimintoa.
Esimerkissämme
x - solu B4 (koska haluamme selvittää ajan, joka kuluu nopeuden ollessa 30 km / tunnissa).
Known_y's - Solu B2 - Solu B3 (Pyörän tunnetulle nopeudelle kulunut aika).
Tunnetut_x - Solu A2 - Solu A3 (jo annetun pyörän nopeus, jolle tiedämme kuluneen ajan).
Joten lopullinen kaava solussa B4 on seuraava:
= FORECAST (A4, B2: B3, A2: A3)
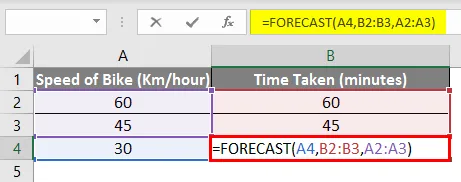
Ja kuten voit nähdä, lopputulos on sama eli 30 minuuttia .
Luo kaavio siirtymällä Lisää-valikkoon napsauttamalla Hajonta ja valitsemalla sitten Hajonta sileillä viivoilla ja merkinnöillä.
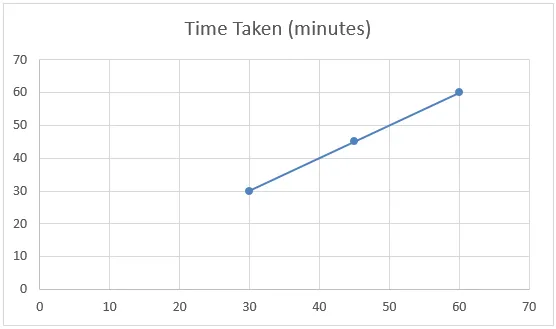
Jos tarkastelemme yllä olevan esimerkin alla olevaa kaaviota, voidaan sanoa, että tietojoukolla on lineaarinen suhde ja joka tunnetaan nimellä lineaarinen interpolointi.
Esimerkkejä lineaarisesta interpoloinnista Excelissä
Ymmärretään lineaarinen interpolointi Excelissä joissain esimerkkeillä.
Voit ladata tämän lineaarisen interpoloinnin Excel-mallin täältä - Lineaarisen interpoloinnin Excel-mallinEsimerkki # 1
Oletetaan, että sinulla on myynti- ja voitotietoja aiemmista vuosista ja haluat tietää kuluvan vuoden voiton, jos saavutat tietyn myyntitason.
Katso alla olevaa taulukkoa. Sinulla on myyntitietoja vuodesta 2016 vuoteen 2018 ja haluat tietää, minkä pitäisi olla voittoa, jos myyntisi on Rs. 40, 00 000 vuonna 2019.
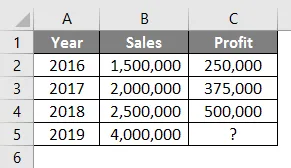
Joten ennustetoiminnon avulla voimme interpoloida vuoden 2019 voiton, kun myynti on Rs. 4000000
Solun C5 kaava on seuraava:
= ENNUSTE (B5, C2: C4, B2: B4)
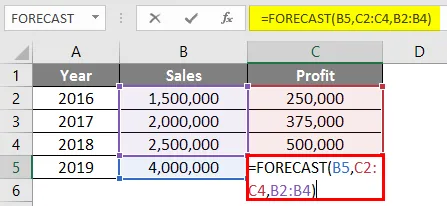
Ennustekaavan käyttämisen jälkeen alla oleva vastaus.
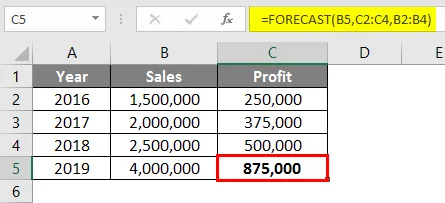
Ennuste-toiminnon tulos on Rs. 875 000 perustuen myyntitietoihin, jotka olivat saatavilla vuosina 2016–2018.
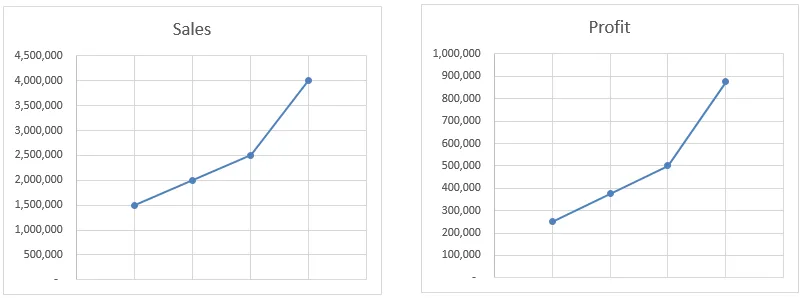
Tässä esimerkissä ennustefunktio interpoloi arvon kaikkien käytettävissä olevien tietojen perusteella eikä vain alkamisen ja päätepisteen perusteella. Kuten kaavioista näet, voitto liikkuu on täsmälleen sama kuin myynti. Vaikka laskemme arvon manuaalisesti, se antaa meille saman tuloksen.
Esimerkki 2
Meillä on tietoja krikettijoukkueen 9 viimeisimmästä ottelusta, joka on ohittanut vartiot ja juoksanut joukkueen maalin.
Haluamme selvittää, kuinka monta juoksua joukkue tekee maalin, jos kahdeksan wicket putoaa.
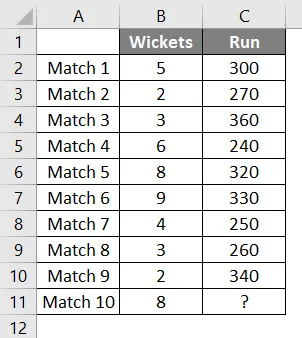
Joten käytämme taas samaa ennustefunktiota kuin yllä.
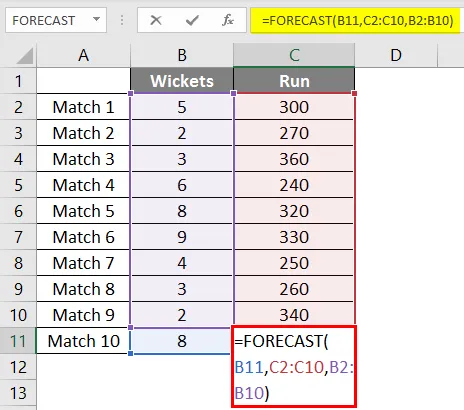
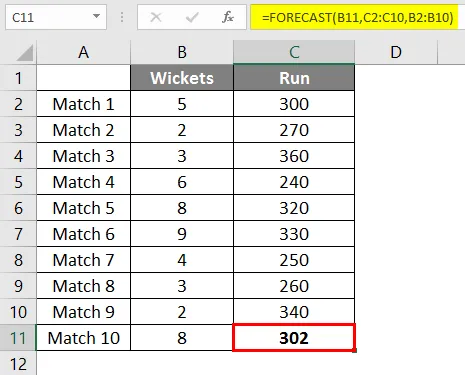
Kaavan soveltamisen jälkeen saamme tuloksen 302 juoksusta, jos 8 wicket putoaa joukkueen pelaamien 9 viimeisen ottelun lineaarisen regression perusteella.
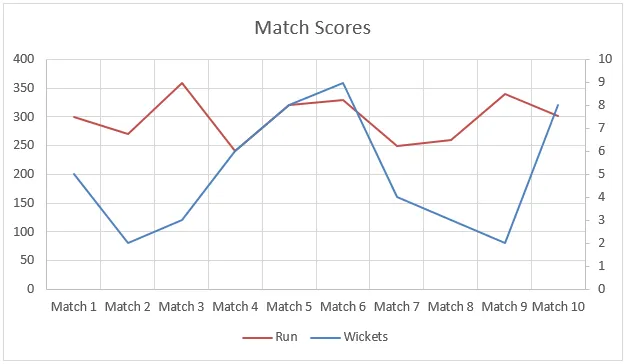
Tässä esimerkissä tiedot eivät olleet lineaarisia, ja voit nähdä sen alla olevasta kaaviosta. Mutta silti ennustetoiminto auttoi meitä interpoloimaan ajoja aiempien otteluiden tietojen avulla.
Muistettavaa tietoa lineaarisesta interpoloinnista Excelissä
- Ennuste-toimintoa käytetään ennustamaan / arvioimaan arvo olemassa olevien arvojen perusteella, mutta se voi myös auttaa interpoloimaan puuttuvan arvon.
- Jos tiedot eivät ole lineaarisia, ennustetoiminto ei anna tarkkaa arvoa, joka perustuu lineaariseen interpolointiin, mutta antaa sinulle lähimmän arvon.
- Jos ennustetoiminnossa x on tekstiä tai ei-numeerista, ennustetoiminto palauttaa #VALUE-virheen.
- Jos Tunnetut_x ja Tunnettu_y eivät sisällä tietoja tai sisältävät erilaisen datapistejoukon, ennustetoiminto antaa # EI / A -virheen.
- Jos Tunnettujen x-arvojen varianssi on nolla, ennustetoiminto antaa # DIV / O-virheen.
Suositellut artikkelit
Tämä on opas Lineaariseen interpolointiin Excelissä. Tässä keskustellaan kuinka lineaarista interpolointia voidaan käyttää Excelissä, sekä käytännön esimerkkejä ja ladattavaa Excel-mallia. Voit myös käydä läpi muiden ehdottamiemme artikkeleidemme -
- Lineaarinen regressio Excelissä
- Etsi tekstiä Excelistä
- Tekstikaava Excel-muodossa
- Marimekko Chart Excel
- Interpoloi Excelissä
- Lineaarinen ohjelmointi Excelissä