Toiminnot R: ssä Erityyppiset funktiot R: ssä syntaksin ja esimerkkien kanssa

Johdatus R: n toimintoihin

Toiminto on määritelty joukko lauseita suorittamaan ja suorittamaan mikä tahansa erityinen looginen tehtävä. Toiminto vie joitain syöttöparametreja, joita kutsutaan argumentiksi suorittaakseen kyseisen tehtävän. Toiminnot auttavat hajottamaan koodin yksinkertaisemmiksi paloiksi organisoimalla sen loogisesti, mikä on helpompi lukea ja ymmärtää. Tässä aiheessa aiomme oppia funktioista R.

Kuinka kirjoittaa funktiot R: hen?

Jos haluat kirjoittaa funktion R, tässä on syntaksi:

Fun_name <- function (argument) (
Function body
)

Täällä voi nähdä ”funktio” -kohtaisia ​​varattuja sanoja käytetään R: ssä minkä tahansa funktion määrittelemiseen. Toiminto ottaa syötteen, joka on argumenttien muodossa. Funktion runko on joukko loogisia lauseita, jotka suoritetaan argumentteilla ja sitten se palauttaa tulosteen. ”Fun_name” on funktiolle annettu nimi, jonka kautta sitä voidaan kutsua mihin tahansa R-ohjelman sijaintiin.

Katsotaanpa esimerkki, joka on selkeämpi funktion käsitteen ymmärtämisessä R: ssä.

R-koodi

Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)

lähtö:

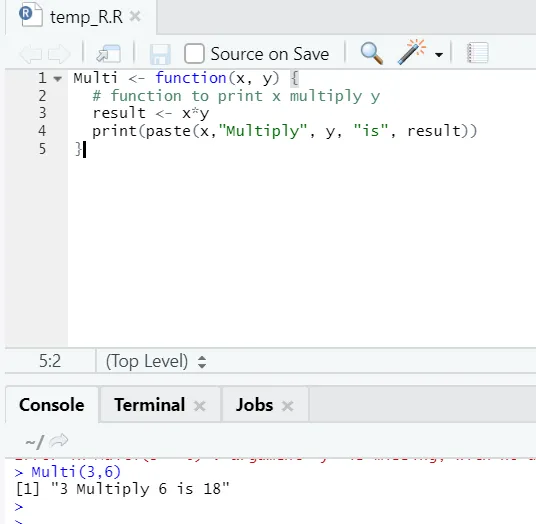
Täällä loimme funktionimen ”Multi”, joka ottaa kaksi argumenttia syötteinä ja tarjoaa moninkertaistetun ulostulon. Ensimmäinen argumentti on x ja toinen argumentti on y. Kuten huomaat, olemme kutsuneet toimintoa nimellä “Multi”. Jos joku haluaa, argumentit voidaan myös asettaa oletusarvoon.

Erityyppiset funktiot R: ssä

Erilaiset R-toiminnot syntaksilla ja esimerkkejä (sisäänrakennettu, matematiikka, tilastollinen jne.)

1) Sisäänrakennettu toiminto -

Nämä ovat R: n mukana tulevia toimintoja osoittamaan tiettyä tehtävää ottamalla argumentti syötteeksi ja antamalla tulos annetun syötteen perusteella. Keskustelemme tässä R: n tärkeistä yleisistä toiminnoista:

a) Lajittelu: Tiedot voivat olla lajiltaan nousevaan tai laskevaan järjestykseen. Tiedot voivat olla, onko jatkuvan muuttujan vektori vai tekijämuuttuja.

Syntaksi:

Tässä on selitys sen parametreista:

• x: Tämä on jatkuvan muuttujan tai tekijämuuttujan vektori
• vähenevä: Tämä voidaan asettaa joko True / False ohjaamaan järjestystä nousevalla tai laskevalla. Oletuksena on FALSE`.
• viimeinen: Jos vektorilla on NA-arvoja, pitäisikö se asettaa viimeiseksi vai ei

R-koodi ja lähtö:

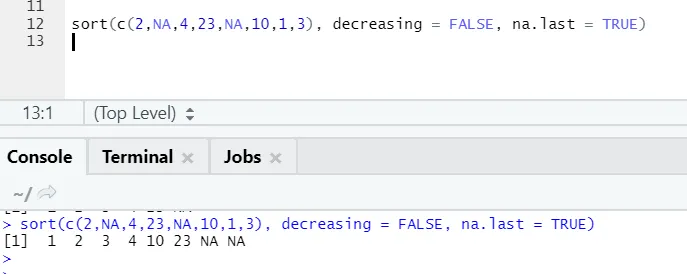
Täällä voidaan huomata, kuinka “NA” -arvot tasautuvat lopussa. Koska parametrimme na.last = True oli totta.

b) Seq: Se tuottaa sekvenssin numerosta kahden määritellyn numeron välillä.

Syntaksi

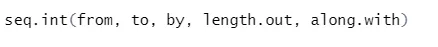
Tässä on selitys sen parametreista:

• alkaen, sekvenssin alku- ja loppuarvoon.
• lisäämällä: Kasvu / ero kahden peräkkäisen numeron välillä
• length.out: sekvenssin vaadittu pituus.
• Yhdessä: viittaa pituuteen tämän argumentin pituudesta

R-koodi ja lähtö:

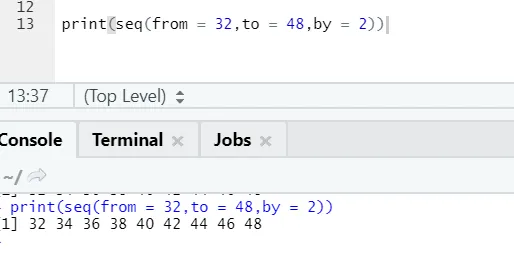
Tässä voidaan huomata, että generoidun sekvenssin inkrementaatio on 2, koska: on määritelty 2: ksi.

c) Toupper, tolower: Kaksi toimintoa: toupper ja tolower ovat merkkijonossa käytettyjä toimintoja, jotta voidaan muuttaa lauseiden kirjainten tapauksia.

R-koodi ja lähtö:

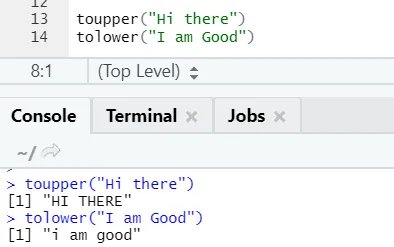
Voidaan huomata, kuinka kirjaintapaukset muuttuvat, kun niitä käytetään funktiossa.

d) Rnorm: Tämä on sisäänrakennettu toiminto, joka tuottaa satunnaislukuja.

R-koodi ja lähtö:

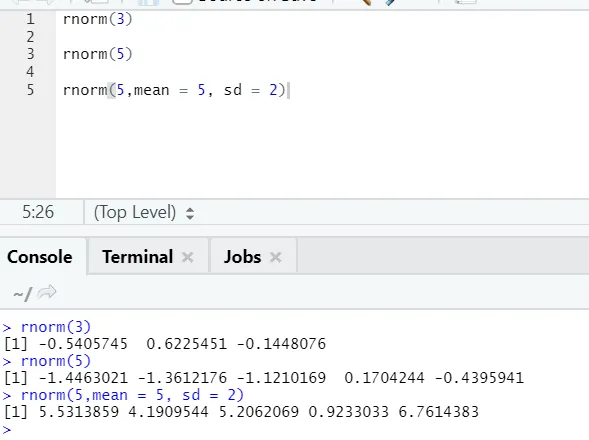
Toiminto rnorm ottaa ensimmäisen argumentin, joka kertoo kuinka monta numeroa on generoitava.

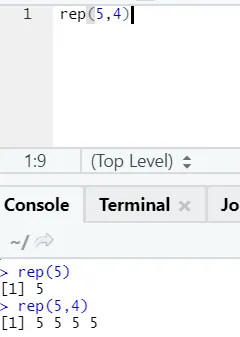
e) Rep: Tämä toiminto toistaa arvon niin monta kertaa kuin on määritelty.

R-syntaksi: rnorm (x, n)

Tässä x edustaa replikoitavaa arvoa ja n edustaa kuinka monta kertaa se on replikoitava.

R-koodi ja lähtö:

f) Liitä: Tämän toiminnon tarkoituksena on yhdistää merkkijonot yhdessä joidenkin tiettyjen merkkien kanssa välillä.

syntaksi

paste(x, sep = “”, collapse = NULL)

R-koodi

paste("fish", "water", sep=" - ")

R-lähtö:

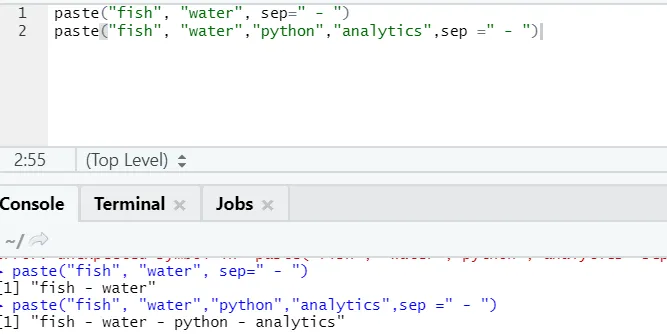
Kuten huomaat, voimme liittää myös enemmän kuin kaksi merkkijonoa. Syyskuu on se erityinen merkki, jonka lisäsimme merkkijonojen väliin. Oletusarvoisesti sep on välilyönti.

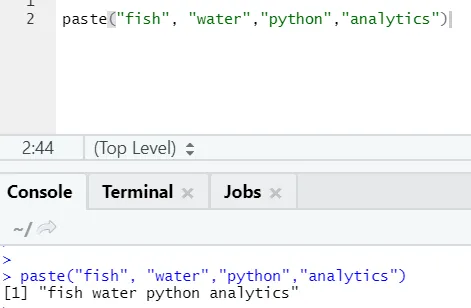
Yksi samanlainen funktio on olemassa kuten tämä, josta kaikkien tulisi olla tietoisia, on paste0.

Toiminto paste0 (x, y, collapse) toimii samalla tavalla kuin paste (x, y, sep = “”, collapse)

Katso alla oleva esimerkki:

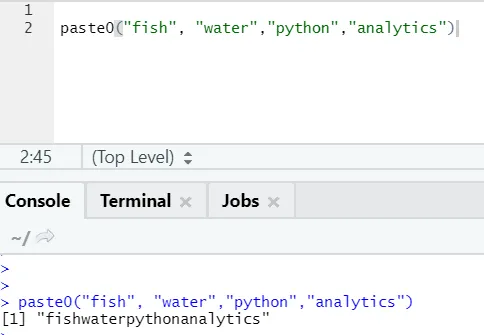
Yksinkertaisin sanoin, tiivistää ja liittää0:

Paste0 on nopeampaa kuin paste, kun kyse on jousien ketjuttamisesta ilman erotinta. Koska liitäntä etsii aina ”sep” ja mikä on siinä oletuksena tilaa.

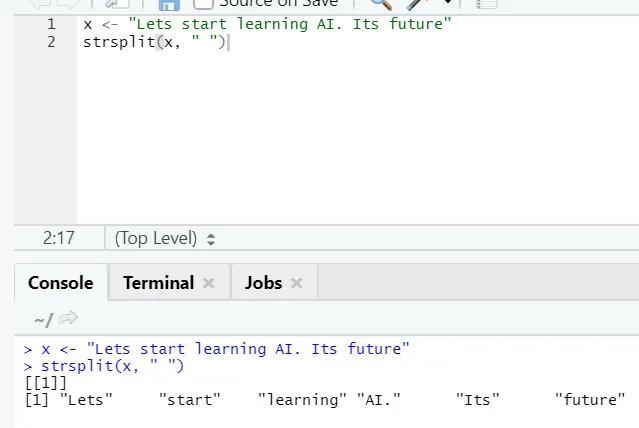
g) Strsplit: Tämä toiminto on jakaa merkkijono. Katsotaanpa yksinkertaisia ​​tapauksia:

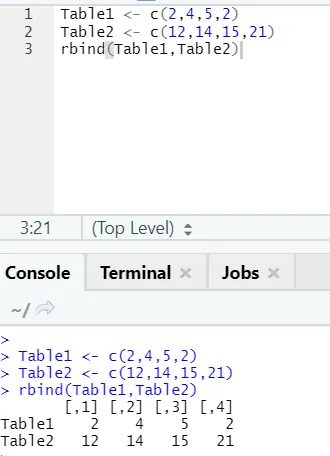
h) Rbind: Toiminto rbind auttaa kammaamaan vektoreita, joilla on sama määrä sarakkeita, yksi toistensa yli.

esimerkki

i) cbind: Tämä yhdistää vektoreita saman määrän rivejä vierekkäin.

esimerkki

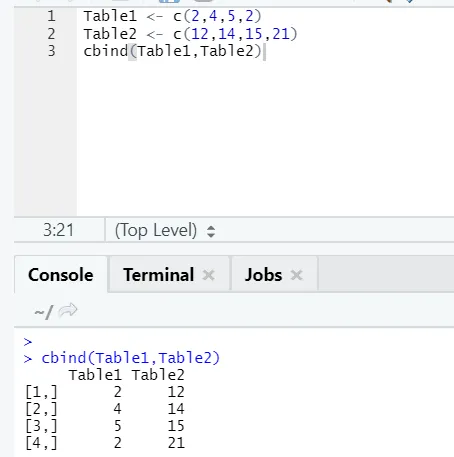
Jos rivien lukumäärä ei vastaa, alla on virhe, jonka löydät:

Sekä cbind että rbind auttavat tietojen käsittelyssä ja muotoilussa.

2) Matematiikka -

R tarjoaa laajan valikoiman matematiikan toimintoja. Katsotaanpa joitain niistä yksityiskohtaisesti:

a) Sqrt: Tämä toiminto laskee numeron tai numeerisen vektorin neliöjuuren.

R-koodi ja lähtö:

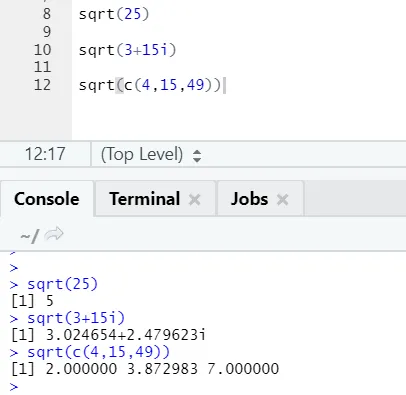
Nähdään kuinka neliöjuuri numero, kompleksiluku ja numeeristen vektorien sekvenssi on laskettu.

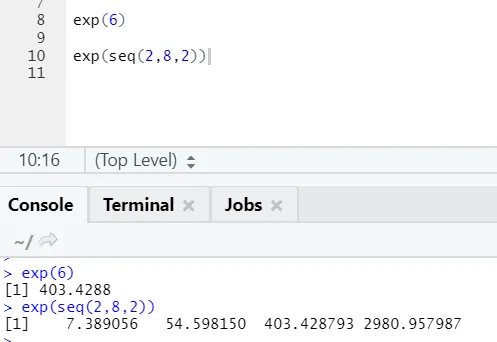
b) Exp: Tämä toiminto laskee numeron tai numeerisen vektorin eksponentiaalisen arvon.

R-koodi ja lähtö:

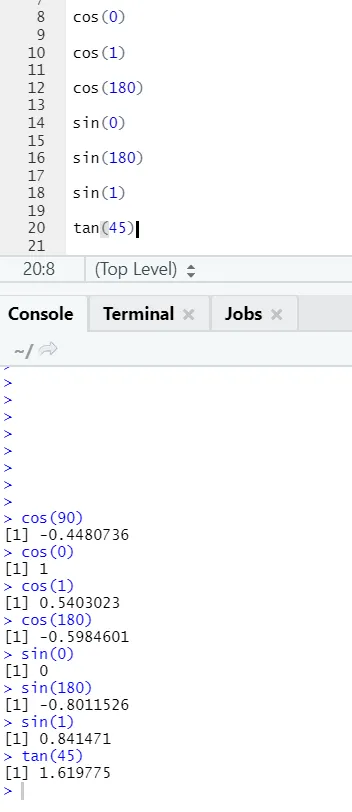
c) Cos, Sin, Tan: Nämä ovat trigonometriafunktioita, jotka toteutetaan tässä R: ssä.

R-koodi ja lähtö:

d) Abs: Tämä toiminto antaa luvun absoluuttisen positiivisen arvon.

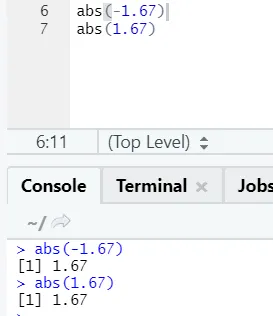
Kuten näette, luvun negatiivinen tai positiivinen palautetaan absoluuttisessa muodossaan. Katsotaan sitä monimutkaiselta numerolta:

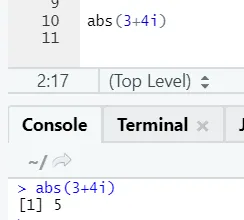
e) Loki: Tämän avulla saadaan luvun logaritmi.

Tässä on alla oleva esimerkki:

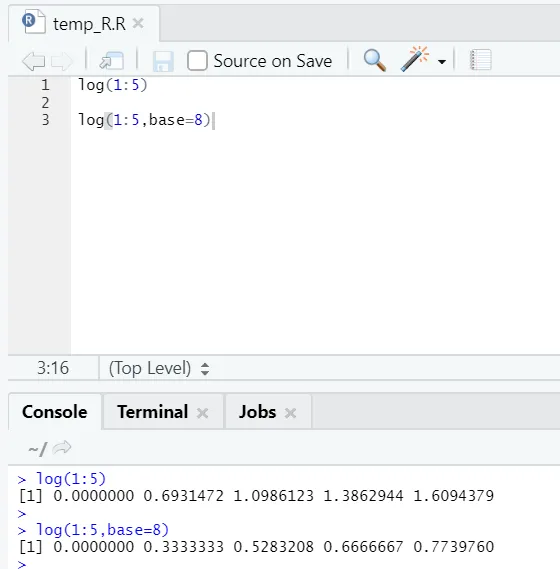
Täällä saadaan joustavuus muuttaa pohjaa vaatimuksen mukaan.

f) Cumsum: Tämä on matemaattinen funktio, joka antaa kumulatiivisia summia. Tässä on alla oleva esimerkki:

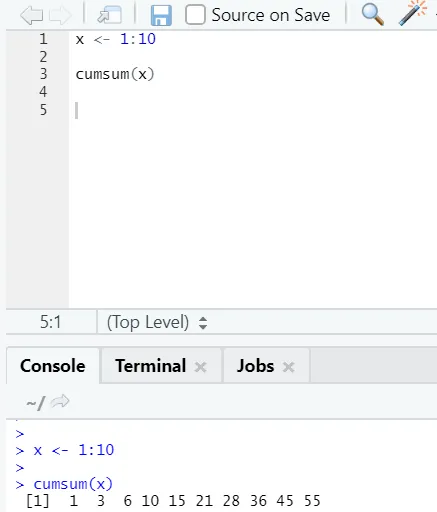
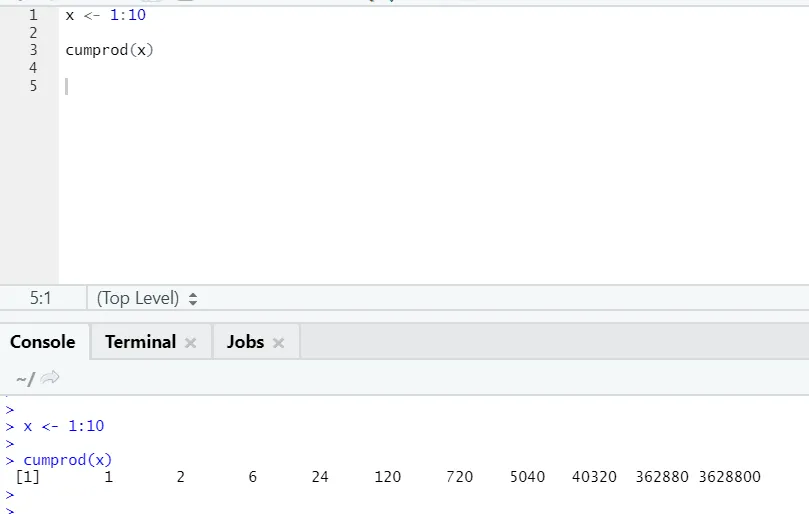
g) Cumprod: Kuten Cumsum-matemaattinen funktio, meillä on cumprod, joissa tapahtuu kumulatiivinen kertolasku.

Katso alla oleva esimerkki:

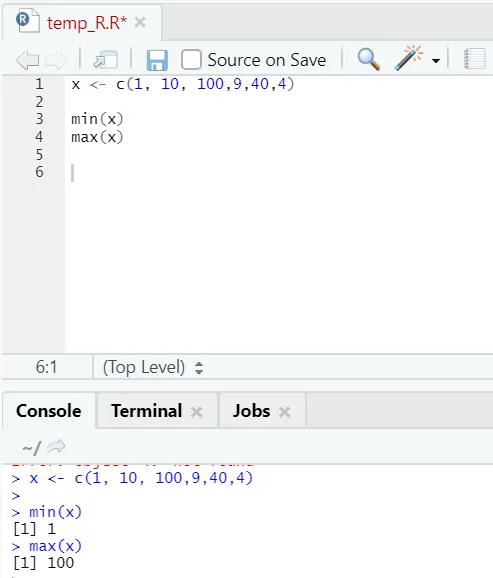
h) Max, Min: Tämä auttaa sinua löytämään suurimman / pienimmän arvon numerojoukosta. Katso alla olevat aiheeseen liittyvät esimerkit:

i) Katto: Katto on matemaattinen funktio, joka tuottaa pienimmän kokonaisluvun määriteltyä suurempi.

Katsotaanpa esimerkkiä:

katto (2, 67)

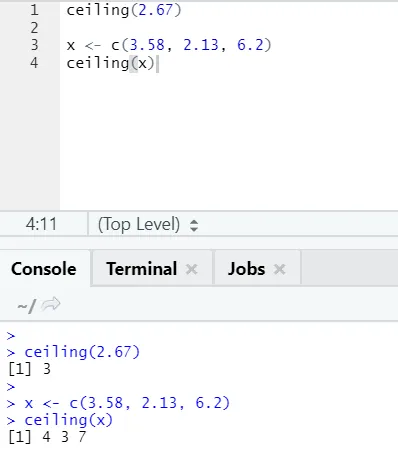
Kuten huomaat, enimmäismäärää sovelletaan sekä lukuun että luetteloon, ja tulo tuli seuraavan suuremman kokonaisluvun pienin.

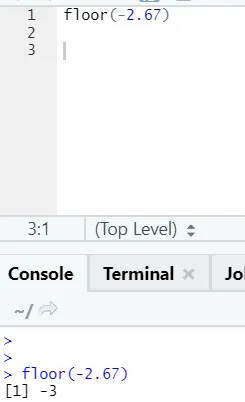
j) Kerros: Kerros on matemaattinen funktio, joka palauttaa määritetyn luvun pienimmän kokonaisluvun.

Seuraava esimerkki auttaa sinua ymmärtämään sitä paremmin:

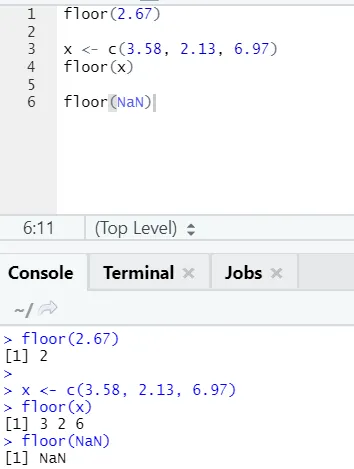
Se toimii samalla tavalla myös negatiivisten arvojen suhteen. Katso, ole hyvä:

3) Tilastotoiminnot -

Nämä ovat funktioita, jotka kuvaavat siihen liittyvää todennäköisyysjakaumaa.

a) Mediaani: Tämä laski mediaanin numerosekvenssistä.

Syntaksi

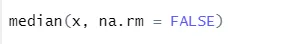
R-koodi ja lähtö:

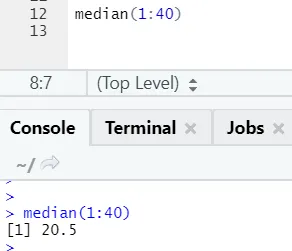
b) Dnorm: Tämä viittaa normaalijakaumaan. Toiminto dnor palauttaa todennäköisyystiheysfunktion arvon normaalijakaumalle, joka on annettu parametreille x, μ ja σ.

R-koodi ja lähtö:

c) Cov: Kovarianssi kertoo, onko kaksi vektoria positiivisesti, negatiivisesti tai täysin ei-sukulaisia.

R-koodi

x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)

R-lähtö:

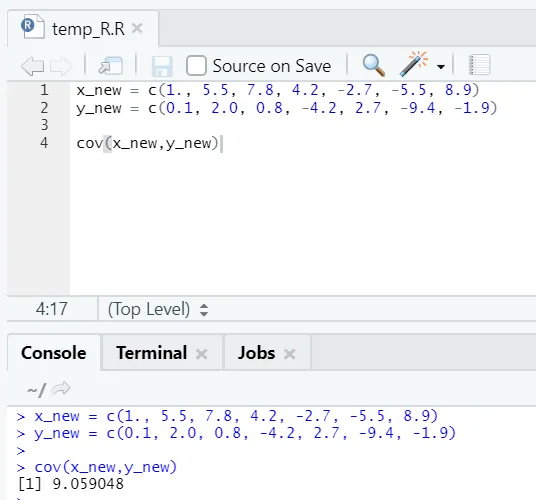
Kuten näette, kaksi vektoria ovat positiivisesti sukua, mikä tarkoittaa, että molemmat vektorit liikkuvat samaan suuntaan. Jos kovarianssi on negatiivinen, se tarkoittaa, että x ja y ovat käänteisesti suhteessa toisiinsa ja liikkuvat siten vastakkaiseen suuntaan.

d) Cor: Tämä on funktio löytää korrelaatio vektoreiden välillä. Se todella antaa kahden vektorin välisen assosiaatiotekijän, joka tunnetaan nimellä “korrelaatiokerroin”. Korrelaatio lisää astekerrointa kovarianssiin nähden. Jos kaksi vektoria korreloivat positiivisesti, korrelaatio kertoo myös kuinka suurella laajuudella ne ovat positiivisesti yhteydessä.

Nämä kolme menetelmätyyppiä, joita voidaan käyttää korrelaation löytämiseen kahden vektorin välillä:

1. Pearson-korrelaatio
2. Kendall-korrelaatio
3. Keihäsmiehen korrelaatio

Yksinkertaisessa R-muodossa se näyttää seuraavalta:

cor(x, y, method = c("pearson", "kendall", "spearman"))

Tässä x ja y ovat vektoreita.

Katsotaanpa käytännöllinen esimerkki sisäänrakennetun tietojoukon korrelaatiosta.

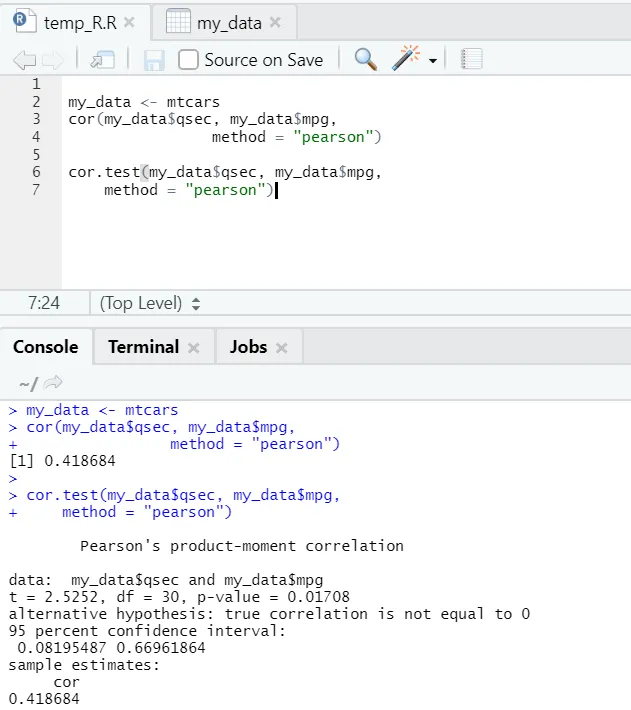
Joten, tässä voit nähdä “cor ()” -funktio antoi korrelaatiokertoimen 0, 41 “qsec”: n ja “mpg” välillä. Kuitenkin on esitelty vielä yksi funktio eli “cor.test ()”, joka ei vain ilmoita korrelaatiokerrointa, vaan myös siihen liittyvää p-arvoa ja t-arvoa. Tulkinta on paljon helpompaa cortesttest-toiminnolla.

Samanlainen voidaan tehdä kahdella muulla korrelaatiomenetelmällä:

R-koodi Pearson-menetelmälle:

my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")

R-koodi Kendall-menetelmälle:

my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")

R-koodi Spearman-menetelmälle:

my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")

Korrelaatiokerroin on välillä -1 ja 1.

Jos korrelaatiokerroin on negatiivinen, se tarkoittaa, että kun x kasvaa, y vähenee.

Jos korrelaatiokerroin on nolla, x-y: n välillä ei ole mitään yhteyttä.

Jos korrelaatiokerroin on positiivinen, se tarkoittaa, että kun x kasvaa, y myös taipumus kasvaa.

e) T-testi: T-testi kertoo, tulevatko kaksi tietojoukkoa samasta (olettaen) normaalijakaumasta vai ei.

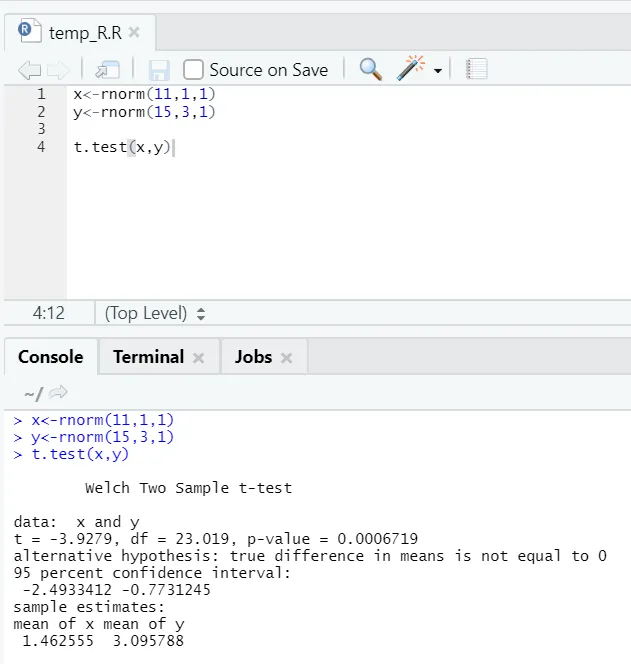
Tässä pitäisi hylätä nollahypoteesi, jonka mukaan kaksi keskiarvoa ovat yhtä suuret, koska p-arvo on alle 0, 05.

Tämä näytetty esimerkki on tyyppiä: parittomat tietojoukot, joiden varianssit ovat epätasaiset. Samoin voidaan kokeilla pariksi muodostetulla aineistolla.

f) Yksinkertainen lineaarinen regressio: Tämä osoittaa suhteen ennustajan / riippumattoman ja vasteen / riippuvan muuttujan välillä.

Yksinkertainen käytännöllinen esimerkki voisi olla ihmisen painon ennustaminen, jos pituus tiedetään.

R-syntaksi

lm(formula, data)

Tässä kaava kuvaa suhdetta tulosteen eli y ja tulomuuttujan elix välillä. Data edustaa tietojoukkoa, johon kaavaa on sovellettava.

Katsotaanpa yksi käytännöllinen esimerkki, jossa lattiapinta-ala on tulomuuttuja ja vuokra on lähtömuuttuja.

x <- c (1510, 1 000, 600, 500, 1280, 136, 1790, 1630)

y <-c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)

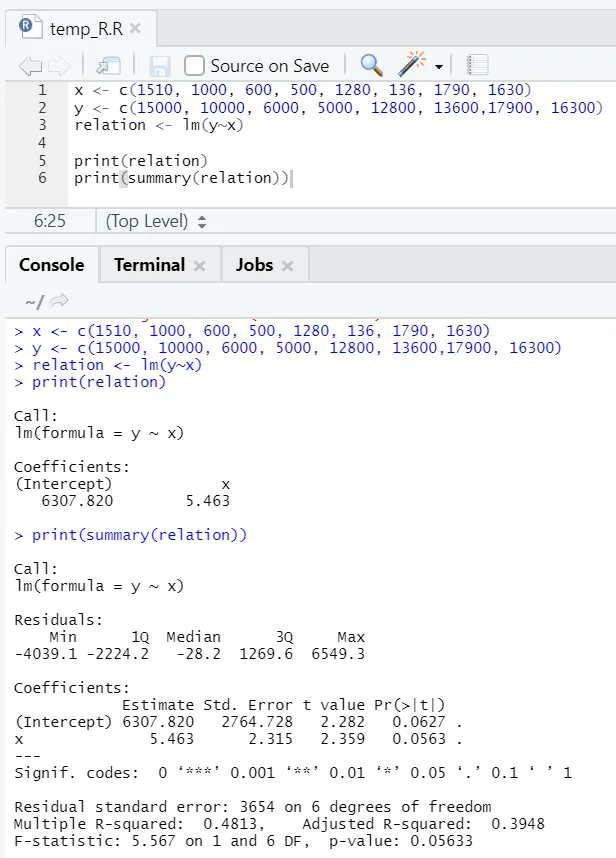
Tässä P-arvo on vähintään 5%. Siksi nollahypoteesiä ei voida hylätä. Pinta-alan ja vuokran suhteen todistamisessa ei ole paljon merkitystä.

Tässä R-neliön arvo on 0, 4813. Tämä tarkoittaa, että vain 48% lähtömuuttujan varianssista voidaan selittää tulomuuttujalla.

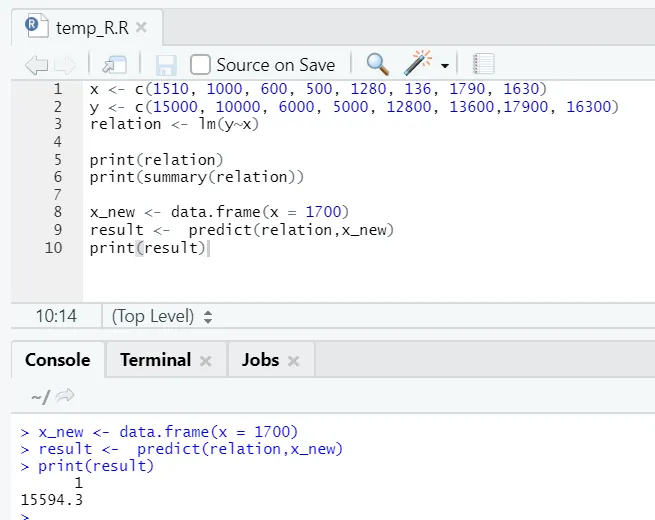
Oletetaan, että meidän on ennustettava lattiapinnan arvo yllä mainitun mallin perusteella.

R-koodi

x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)

R-lähtö:

Yllä olevan R-koodin suorittamisen jälkeen lähtö näyttää seuraavalta:

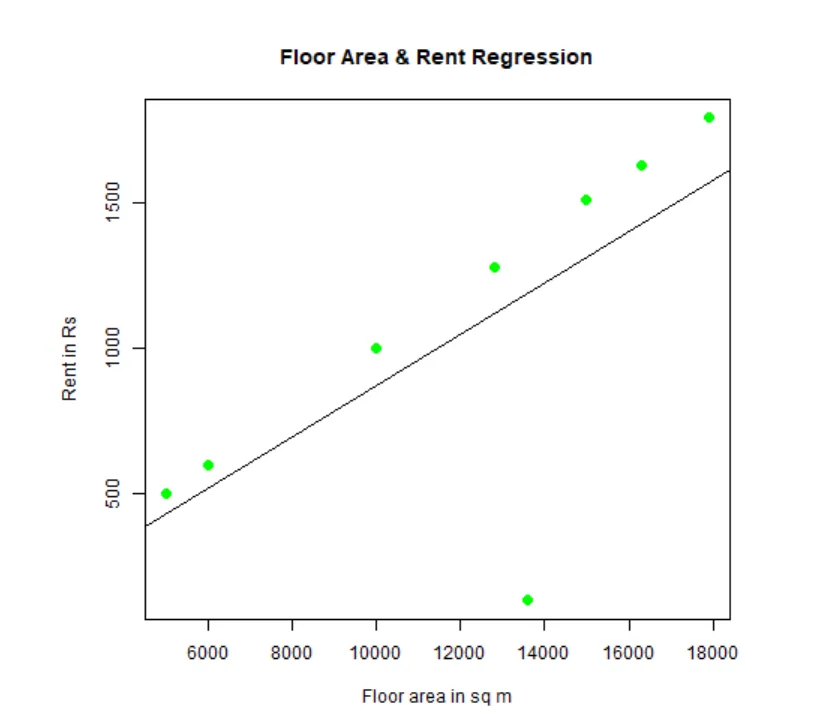
Regression voi sovittaa ja visualisoida. Tässä on R-koodi tälle:

# Anna png-kaavotiedostolle nimi.

png(file = "LinearRegressionSample.png.webp")

# Piirrä kaavio.

plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")

# Tallenna tiedosto.

dev.off()

Tämä “LinearRegressionSample.png.webp” -diagrammi luodaan nykyiseen työhakemistoon.

g) Chi-neliötesti

Tämä on tilastollinen funktio R: ssä. Tämä testi pitää tärkeänä todistaakseen, esiintyykö korrelaatio kahden kategorisen muuttujan välillä.

Tämä testi toimii myös kuten kaikki muut tilastolliset testit, jotka perustuivat p-arvoon, voidaan hyväksyä tai hylätä nollahypoteesi.

R-syntaksi

chisq.test(data), /code>

Katsotaanpa yksi käytännöllinen esimerkki siitä.

R-koodi

# Lataa kirjasto.

library(datasets)
data(iris)

# Luo tietokehys pääaineistosta.

iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)

# Luo taulukko tarvittavilla muuttujilla.

iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)

# Suorita Chi-Square-testi.

print(chisq.test(iris.data))

R-lähtö:

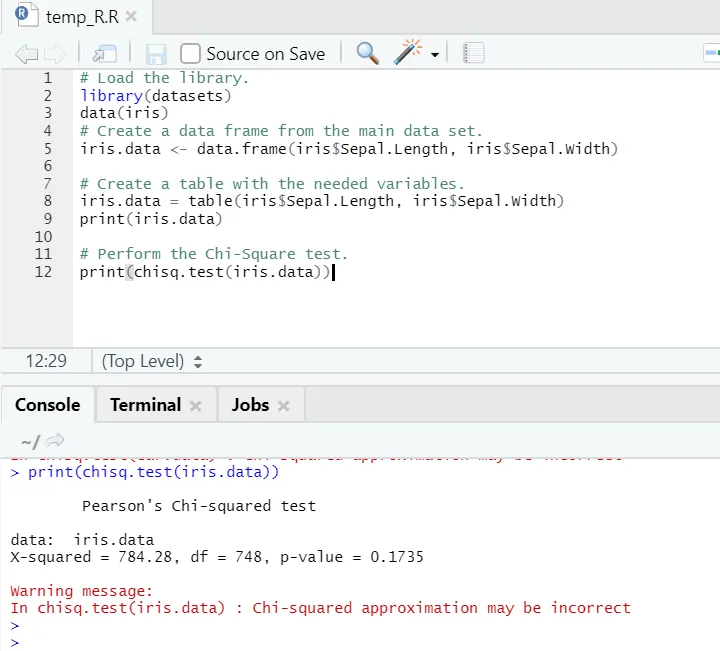
Kuten voidaan nähdä, chi-neliötesti on suoritettu iriksen tietojoukolla, ottaen huomioon sen kaksi muuttujaa “Sepal. Pituus ”ja” Sepal.leveys ”.

P-arvo on vähintään 0, 05, joten näiden kahden muuttujan välillä ei ole korrelaatiota. Tai voimme sanoa, että nämä kaksi muuttujaa eivät ole riippuvaisia ​​toisistaan.

johtopäätös

R-toiminnot ovat yksinkertaisia, helppo asentaa, helppo tarttua ja silti erittäin tehokkaita. Näimme R.: ssä erilaisia ​​toimintoja, joita käytetään osana perustietoa. Kun nämä edellä mainitut toiminnot ovat tyytyväisiä, voidaan tutkia muita erilaisia ​​toimintoja. Toiminnot auttavat sinua saamaan koodisi ajoon yksinkertaisella ja tiiviillä tavalla. Toiminnot voivat olla sisäänrakennetut tai käyttäjän määrittelemät. Kaikki riippuu tarpeesta käsitellessään ongelmaa. Toiminnot antavat ohjelmalle hyvän muodon.

Suositellut artikkelit

Tämä on opas R.: n funktioihin. Tässä keskustellaan siitä, kuinka funktiot kirjoitetaan R: ssä ja erityyppiset funktiot R: ssä syntaksin ja esimerkkien avulla. Voit myös tarkastella seuraavaa artikkelia saadaksesi lisätietoja -

1. R-kielen toiminnot
2. SQL-merkkijonotoiminnot
3. T-SQL-merkkijonotoiminnot
4. PostgreSQL-merkkijonotoiminnot