
Määrityskertoimen kaava (sisällysluettelo)
- Kaava
- esimerkit
Mikä on määrityskertoimen kaava?
Tilastossa määrityskerroin, jota kutsutaan myös R2: ksi, on työkalu, joka määrittelee ja arvioi tilastomallin kykyä selittää ja ennustaa tulevia tuloksia. Toisin sanoen, jos meillä on mallissa riippuvainen muuttuja y ja riippumaton muuttuja x, niin R2 auttaa määrittämään y: n variaatio variaation x avulla. Se on yksi regressioanalyysin tärkeimmistä tuotoksista, ja sitä käytetään, kun haluamme ennustaa tulevaisuutta tai testata joitain malleja, joilla on siihen liittyvää tietoa. R2: n arvo on välillä 0 ja 1 ja sitä suurempi on R2: n arvo, sitä parempi on mallin ennuste ja vahvuus. R 2 on hyvin samanlainen kuin korrelaatiokerroin, koska korrelaatiokerroin mittaa kahden muuttujan suoraa assosiaatiota. R2 on periaatteessa korrelaatiokertoimen neliö.
Määrityskertoimen kaava:
Määrityskertoimen laskemiseksi on olemassa useita kaavoja:
- Korrelaatiokertoimen käyttö:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Missä:
- X - tietopisteet tietojoukossa X
- Y - tietopisteet tietojoukossa Y
- X m - tietojoukon X keskiarvo
- Y m - tietojoukon Y keskiarvo
Niin
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Regressioulostulojen käyttäminen
Määrityskerroin (R 2 ) = selitetty variaatio / kokonaisvaihtelu
Määrityskerroin (R 2 ) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Missä:
- TSS - neliöiden kokonaissumma = Σ (Yi - Ym) 2
- MSS - neliöiden mallisumma = Σ (Y - Ym) 2
- RSS - neliöiden jäännössumma = Σ (Yi - Y ^) 2
Y on mallin ennustettu arvo, Yi on i-arvo ja Ym on keskiarvo
Esimerkkejä määrityskertoimen kaavasta (Excel-mallilla)
Otetaan esimerkki ymmärtää determinaatiokertoimen laskenta paremmin.
Voit ladata tämän määrityskertoimen Formula Excel -mallin täältä - Määrityskertoimen Formula Excel TemplateMäärityskertoimen kaava - esimerkki # 1
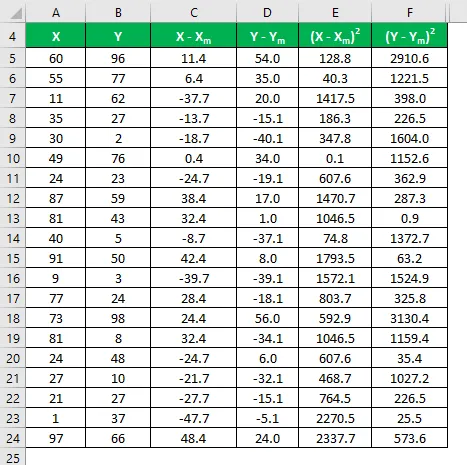
Oletetaan, että meillä on kaksi tietojoukkoa X & Y ja kukin sisältää 20 satunnaista datapistettä. Laske määrityskerroin tietojoukolle X & Y.
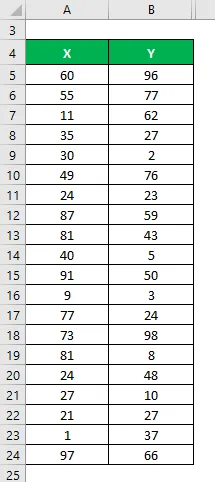
Keskiarvo lasketaan seuraavasti:
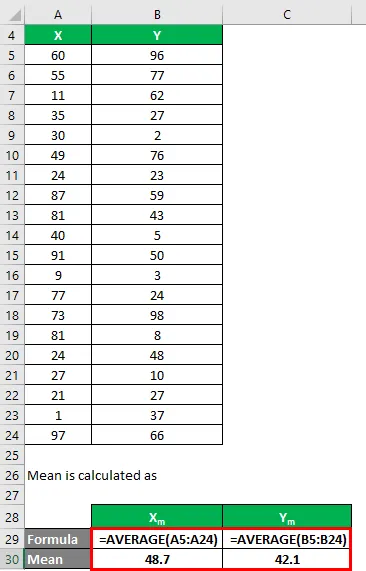
- Tietojoukon X keskiarvo = 48, 7
- Tietojoukon keskiarvo Y = 42, 1
Nyt meidän on laskettava ero datapisteiden ja keskiarvon välillä.
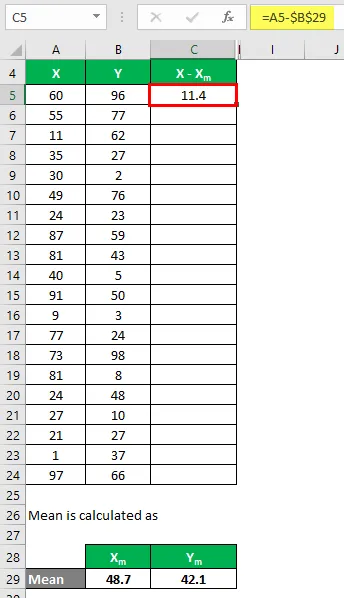
Samoin laske kaikki X: n tietojoukot.
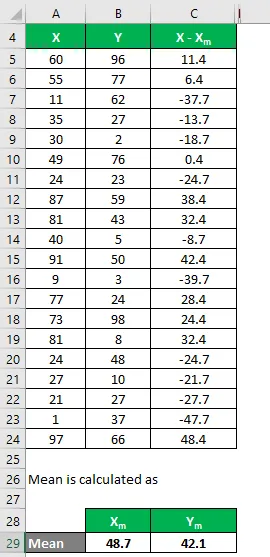
Laske se samalla tavalla myös tietojoukolle Y.

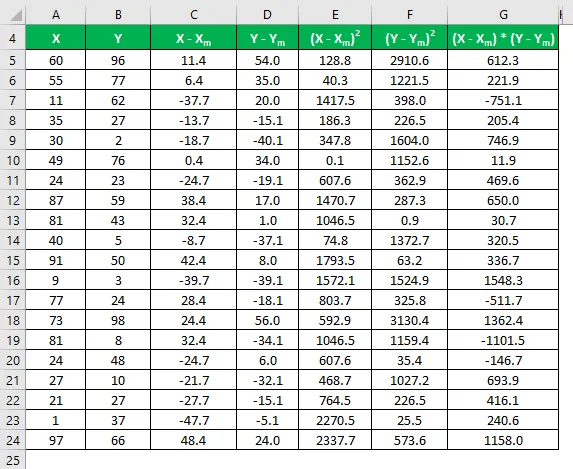
Laske eron neliö molemmille tietojoukoille X ja Y.
Kertoke ero X: ssä Y: llä.
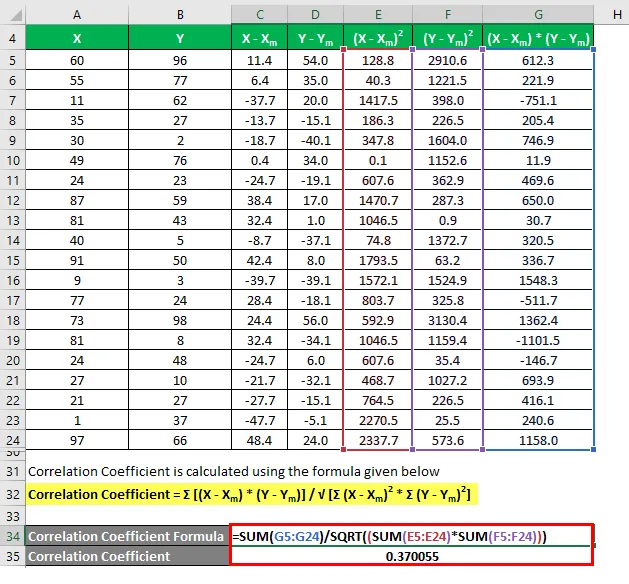
Korrelaatiokerroin lasketaan alla olevan kaavan avulla
Korrelaatiokerroin = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
Määrityskerroin lasketaan alla olevan kaavan avulla
Määrityskerroin = (korrelaatiokerroin) 2
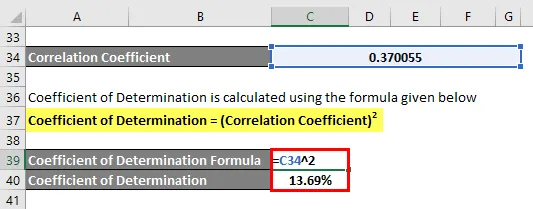
Määrityskerroin = 13, 69%
Määrityskertoimen kaava - esimerkki 2
Sanotaan, että olet erittäin riskitön sijoittaja ja haluat sijoittaa rahaa osakemarkkinoille. Et ole varma mihin osakkeisiin haluat sijoittaa, ja myös riskihalu on alhainen. Joten haluat sijoittaa osakean, joka on turvallinen ja voi jäljitellä indeksin suorituskykyä. Ystäväsi, joka on aktiivinen sijoittaja, on valinnut sinulle 3 osakekantaa perus- ja teknisten tietojen perusteella ja haluat valita 2 osaketta näistä kolmesta.
Olet myös kerännyt tietoja heidän historiallisista tuottoistaan viimeisen 15 vuoden ajalta.
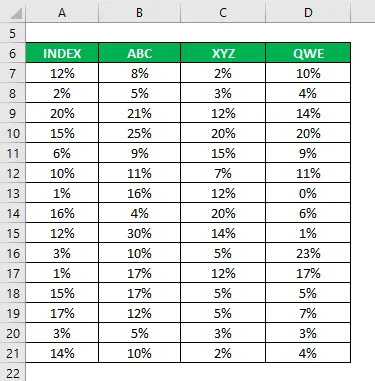
Korrelaatiokerroin lasketaan käyttämällä excel-kaavaa
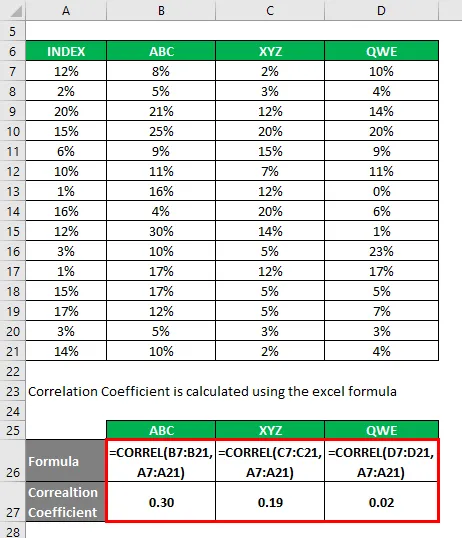
Määrityskerroin lasketaan alla olevan kaavan avulla
Määrityskerroin = (korrelaatiokerroin) 2
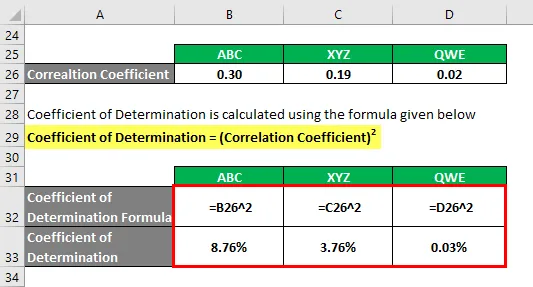
Tietojen perusteella valitset sijoitettavat osakekannat ABC ja XYZ, koska niillä on suurin määrityskerroin.
Selitys
Määrityskerroin, kuten edellä selitettiin, on kahden tietojoukon välisen korrelaation neliö. Jos R2 on 0, se tarkoittaa, että korrelaatiota ei ole ja riippumaton muuttuja ei voi ennustaa riippuvaisen muuttujan arvoa. Samoin, jos sen arvo on 1, se tarkoittaa, että riippumaton muuttuja on aina onnistunut ennustamaan riippuvainen muuttuja. Mutta on myös joitain rajoituksia. Vaikka se kertoo meille kahden tietojoukon korrelaation, se ei kerro, riittääkö tämä arvo vai ei.
Myös suuri arvo R2 ei aina tarkoita, että kahdella muuttujalla on vahvat suhteet ja se voi olla fluke. Esimerkiksi: Oletetaan, että R2: n arvo vuoden aikana myytyjen autojen ja vuodessa myytävien jäätelölaatikoiden välillä on 80%. Mutta näiden kahden välillä ei ole yhteyttä. Joten pitäisi olla erittäin varovainen käyttäessäsi R2: ta ja ymmärtää ensin tiedot ja sitten soveltaa menetelmää
Määrityskertoimen kaavan relevanssi ja käyttö
R2: lla on monia käytännön sovelluksia. Esimerkiksi sijoittajat käyttävät R2: ta erittäin yleisesti vertailemaan salkunsa kehitystä markkinoihin ja yrittämään ennustaa myös tulevia suuntauksia. Samoin riskipääomarahastot käyttävät R 2: ta auttaa heitä mallintamaan riskiä malleissaan. Mutta lopulta lopputulos perustuu puhtaisiin lukuihin ja tilastoihin, jotka voivat joskus olla harhaanjohtavia. Kuten edellä mainittiin, on ensin tarkistettava, onko R2: n tuloksella järkevää tosielämässä vai ei.
Suositellut artikkelit
Tämä on opas määrityskertoimen kaavaan. Tässä keskustellaan siitä, kuinka määritettävyyskerroin lasketaan yhdessä käytännön esimerkkien ja ladattavan excel-mallin kanssa. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Opas markkinariskin premium-kaavaan
- Esimerkkejä kattavuussuhteen kaavasta
- Laskuri toimintopohjaiseen kustannuslaskelmaan
- Kuinka laskea tietosuhde kaavaa käyttämällä?