Johdanto kasalajitteluun C: ssä
Lajittelu on tekniikka, joka liittyy elementtien järjestykseen eri ominaisuuksien perusteella. (Ominaisuudet, kuten tietojen järjestäminen nousevassa, laskevassa tai aakkosjärjestyksessä). Yksi merkittävä esimerkki lajittelusta, jota voimme ajatella täällä, on tavaroiden tilaaminen verkkokaupoissa. Voimme suhtautua hintoihin, suosioon, viimeisimpiin ja niin edelleen. Joten on olemassa monia tekniikoita elementtien sijoittamiselle lajittelun avulla. Tässä aiheessa aiomme oppia Heap Sort in C.
Täällä opitaan yksi yleisimmistä lajittelumenetelmistä, Heap Sort, C-ohjelmointikielen kautta.
Heap Sortin logiikka
Kuinka oikeasti voimme suorittaa kasalajittelu? Katsotaanpa alla.
Ensinnäkin kasa on yksi puupohjaisesta tietorakenteesta. Tässä mukana oleva puu on aina täydellinen binaaripuu. Ja kasa on olemassa kahdenlaisia
- Min - Heap: Yleensä järjestetty nousevaan järjestykseen, ts. Jos emosolmun elementin arvo on pienempi kuin alaisolmun elementtien.
- Max - Heap: Yleensä järjestetty alenevassa järjestyksessä, ts. Jos emosolmun elementillä on arvo enemmän kuin alaissolmun elementteillä.
Vaiheet kasalajitteluun
- Kun lajittelematon luettelotieto on saatu, elementit järjestetään kasan datarakenteeseen joko perustuen min- tai max-kasan luomiseen.
- Yllä olevan luettelon ensimmäinen elementti lisätään taulukkoomme
- Jälleen muodostetaan päätietojen rakennetekniikka, joka on sama kuin ensimmäinen vaihe, ja taas joko korkein tai vähiten elementti otetaan ja lisätään joukkoomme.
- Toistetut vaiheet auttavat meitä saamaan taulukon lajiteltuun luetteloon.
Ohjelma kasaan lajittelu C: ssä
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Ensinnäkin pyydämme käyttäjää syöttämään lajittelemiseen käytettävien elementtien lukumäärän ja sitten käyttäjän sallitaan kirjoittaa erilaisia lajiteltavia elementtejä.
Seuraavat vaiheet
- Seuraavaksi keskitymme luomaan kasarijärjestelmä, tässä tapauksessa max-kasan taulukko.
- Tärkein ehto maksimikasarijonojen saamiseksi on tarkistaa, ettei mikään vanhemmasolmun arvo ole pienempi kuin sen alaissolmun arvo. Aiomme vaihtaa, kunnes saavutamme tämän ehdon.
- Tärkein etu tässä täydellisessä binaaripuussa on, että emosolmun vasempaan ja oikeaan solmuun voidaan päästä arvoilla 2 (i) + 1 ja 2 * (i) + 2, vastaavasti. Missä olen vanhemmasolmu.
- Joten tällä tavalla täällä, sijoitamme juurisolmun, joka sisältää maksimiarvon, oikeimpaan lehtisolmupaikkaan. Ja sitten uudelleen noudattaen samaa menettelyä siten, että seuraavasta enimmäismäärästä tulee nyt juurisolmu.
- Aiomme seurata samaa menettelyä, kunnes kasaan matriisissa on jäljellä vain yksi solmu.
- Ja sitten järjestämme kasaarjamme muodostamaan täydellisen lajitellun matriisin kasvavassa järjestyksessä.
- Lopuksi tulostamme lajiteltua taulukkoa tulosteen.
lähtö:
Lähtö on kiinnitetty alla.
Saanen näyttää teille kuvallisen esityksen tapahtumista:
- Syötetty data esitetään ensin yhden ulottuvuuden taulukon muodossa seuraavasti.

- Muodostuneen binaaripuun kuvakuva on seuraava:
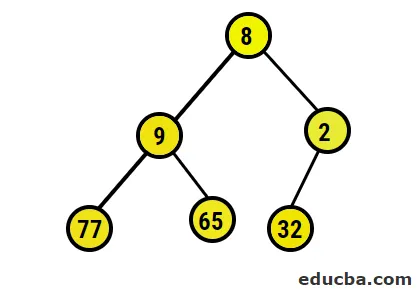
- Nyt aiomme muuntaa maksimikasanon varmistamalla, että kaikki vanhemman solmut ovat aina suurempia kuin lapsisolmut. Kuten kasassa lajiteltujen ryhmien tulostuksessa mainittiin, kuvallinen esitys olisi:
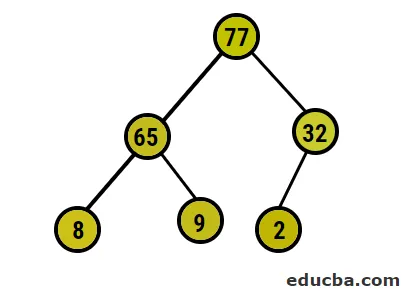
- Tämän jälkeen aiomme vaihtaa juurisolmun äärimmäisen lehden solmun kanssa ja poistaa sen sitten puusta. Lehdesolmu olisi juuri juuri nyt ja uudelleen sama prosessi e seurata saadaksesi jälleen korkein elementti juuressa
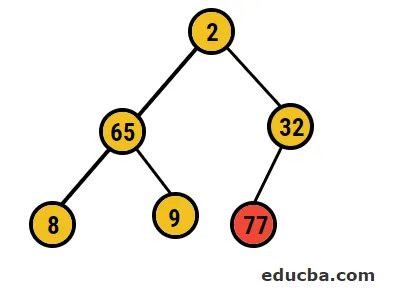
- Joten tässä tapauksessa 77 numeroa poistetaan tästä puusta ja sijoitetaan lajiteltuun taulukkoomme ja prosessi toistetaan.
Edellä olemme nähneet sen muodostavan maksimikasan taulukon. Samaa prosessia käsitellään myös min-kasan taulukon muodostamisessa. Kuten edellä käsiteltiin, ainoa ero on vanhempien ja lasten solmuelementtien välisessä suhteessa.
Voitko yrittää harjoitteluna muodostaa kasalajittelu alenevassa järjestyksessä?
johtopäätös
Vaikka lajittelumenetelmiä on monia, kasalajittelua pidetään yhtenä parempana lajittelumenetelmänä ajan ja tilan monimutkaisuuden vuoksi. Aikakompleksiisuus kaikkien parhaimpien, keskimääräisten ja pahimpien tapausten suhteen on O (nlogn), missä pahimman tapauksen monimutkaisuus on parempi kuin Quicksortin pahimman tapauksen monimutkaisuus ja tilan monimutkaisuus on O (1).
Suositellut artikkelit
Tämä on opas kasettien lajitteluun C. Tässä keskustellaan kasan lajittelun logiikasta ja vaiheista näytteen koodin ja tulosteen kanssa sekä kuvan esitykset. Saatat myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Kasa lajittelu Java
- Valinta Lajittele Java
- Palindromi C-ohjelmassa
- Kuviot C-ohjelmoinnissa
- Kasa lajittelu C ++: ssa (algoritmi)
- Heap Sort Pythonissa
- C Matriisin kertolaskun ohjelmointi