
Johdatus matematiikan toimintoihin C: ssä
Tässä artikkelissa luetellaan C-ohjelmointikielissä käytetyt erilaiset matemaattiset toiminnot ja toimiva koodikuva. Tietokoneet tekevät valtavia matemaattisia laskelmia ja analyysejä valtavista lukuista, joten olemme käyttäneet matematiikkaominaisuuksia C: ssä. Ennen kuin aloitat, meidän on tiedettävä, että C-kielet käyttävät otsikkoa / kirjastoa Math.h nimeltään erilaisille matemaattisille toiminnoille. Tämä auttaa laskemaan trigonometriset operaatiot, logaritmit, absoluuttiset arvot, neliöjuuret. Joten tutkitaan siis tässä kirjastossa käytettyjä erityyppisiä toimintoja. Kaikki nämä toiminnot ovat kaksinkertaisia tietotyyppinä ja palauttavat saman.
Erilaiset matematiikan toiminnot C: ssä
Katsotaanpa, että math.h: ssa on määritelty erilaisia toimintoja, ja matematiikkakirjasto on luokiteltu kolmeen päätyyppiin: trigonometriset funktiot, matemaattiset funktiot, loki / expo-funktiot. Alla olevien toimintojen toteuttamiseksi on pakollista sisällyttää tai koodiin.
1. kerros (kaksinkertainen a)
Tämä toiminto palauttaa suurimman kokonaisluvun, joka ei ole suurempi kuin 'a'. Se pyöristää arvon ja tuottaa kaksinkertaisen tuloksen. Se käyttäytyy eri tavalla negatiivisten lukujen suhteen, kun ne pyöristyvät seuraavaan negatiiviseen lukuun.
Esimerkki: kerros (7.2) on 7, 0
kerros (-7, 2) on -8, 0
Esimerkki:
Tämä ohjelma kuvaa kuinka laskea ilmoitetun arvon kerros ja pyöristetään seuraavaan arvoon 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
lähtö:

2. ceil ()
Syntaksi:
double ceil (double b)
Tämä toiminto palauttaa pienimmän kokonaisluvun, joka on suurempi tai yhtä suuri kuin b, ja pyöristää arvon ylöspäin. Negatiivisen arvon tapauksessa se siirtyy vasemmalle. Esimerkki 3.4 tuottaa -3: lla on lähtö.
Esimerkki:
Tämä ohjelma selittää ottamalla huomioon kelluva argumentti ja palauttaa kattoarvon.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
lähtö:

3. Sqrt ()
Tämä toiminto palauttaa määritetyn luvun neliöjuuren.
Syntaksi:
sqrt( arg)
Esimerkki:
Alla oleva koodi selittää tunnetuimman matemaattisen funktion sqrt () ottamalla 'n' arvot laskemaan neliöjuuren eri 'n' -arvoille.
#include
#include
int main()
(
double n, output;
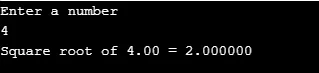
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
lähtö:
4. pyöreä ()
Tämä toiminto pyöristää tietyn tulon lähimmän arvon. Se poistaa virheen, jos arvo on liian suuri. Muut toiminnot, kuten lround (), llround (), pyöristävät myös lähimmän kokonaisluvun.
Syntaksi:
int round(arg)
Esimerkki:
Alla oleva koodi on hyvin yksinkertainen, joka pyöristyy lähimpään r-arvoon for-silmukassa.
#include
#include
int main ()
(
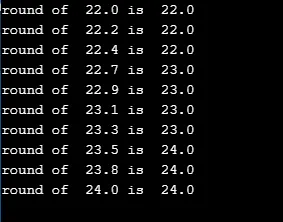
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
lähtö:
5.sivut ()
Tämä toiminto palaa annettuun numeroon (a b ). Se palauttaa korotetun b: n tehoon, jolla on kaksi parametripohjaa ja eksponentti.
Esimerkki:
Alla olevassa lähdekoodissa sallimme käyttäjän syöttää syöttöarvon laskeaksi annettujen kahden argumentin teho.
#include
#include
int main()
(
int r, ba, expr;
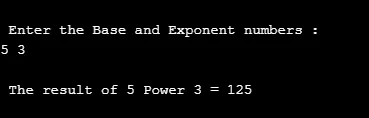
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
lähtö:
6. runko ()
Tämä toiminto auttaa katkaisemaan annetun arvon. Se palauttaa kokonaislukuarvot. Kelluvien ja kaksinkertaisten arvojen katkaisemiseksi käytetään truncf (), truncl ().
Syntaksi:
double trunc(a);
Esimerkki:
Lähdekoodin alapuolella on kaksi syöttöarvoa a, b katkaistakseen kaksinkertaiset arvot.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
lähtö:

7. fmod ()
Tämä toiminto palauttaa jäljelle jäävän annetun kahden tuloarvon, kun m jaetaan n: llä.
Syntaksi:
double fmod(double I, double j)
Esimerkki:
Alla olevassa esimerkissä käyttäjältä tarvitaan kaksi arvoa lopun laskemiseksi fmod () -toiminnolla.
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
lähtö:

Trigonometriset toiminnot
Alla on trigonometrisen toiminnot:
1. synti ()
Tämä sisäänrakennettu toiminto antaa annetun luvun siniarvon, laskee liukulukujen arvot. asin () laskee kaaren, hyperboliseksi se on sinh ().
Syntaksi:
return type sin(y);
y palauttaa arvon radiaaneina ja paluutyyppi vie kaksinkertaisen arvon.
Esimerkki:
Seuraavassa lähdekoodissa olen ottanut kaksi erilaista tuloarvoa synnin arvon laskemiseksi ja palauttaa kaksinkertaisen.
#include
#include
int main()
(
double a;
double z;
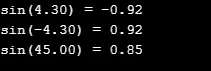
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
lähtö:
2. sinh ()
Tämä matemaattinen funktio laskee trigonometrisen tangentin siniarvon annetulle numerolle.
Syntaksi:
double sinh(x);
esimerkki
Alla olevassa lähdekoodissa sinihyperboolia lasketaan ilmoittamalla tuloarvo.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
ulostulo

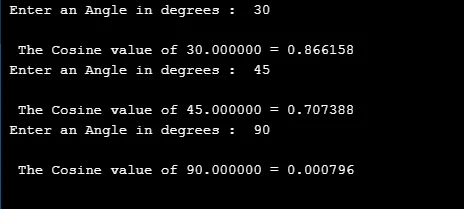
3. cos ()
Tämä matemaattinen funktio määrittää annetun elementin trigonometrisen kosinin arvon.
Syntaksi: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
lähtö:
4. cosh ()
Se palauttaa hyberbolisen kosinuksen tietylle arvolle.
Syntaksi:
double cosh(y);
esimerkki
Seuraava esimerkki osoittaa, että hyperbolisen laskentaan tarvitaan kaksi erilaista tuloarvoa.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
ulostulo

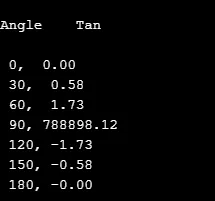
5. rusketus ()
Tämä matemaattikirjastofunktio laskee matemaattisen lausekkeen kulman tangenttiset arvot ja mitataan radiaaneina.
Se voidaan julistaa
double tan(arguments);
esimerkki
Seuraavassa lähdekoodissa tan-arvo lasketaan seuraaville kulmille, joita lisätään käyttämällä silmukkaa.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
lähtö:
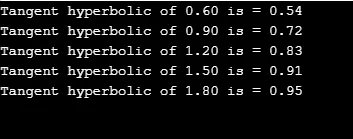
6. tanh ()
tanh ()-funktio palauttaa annetun arvon hyperbolisen tangentin. Se vie yhden parametrin. Pitkän kaksinkertaisen tangentin löytämisen lisäksi laskentaan käytetään tanhlia () ja tanhfia ().
Syntaksi:
double tanh( val);
Esimerkki:
J-arvoille lasketaan tangentti hyberbolinen silmukoita varten. Katsotaan kuinka se toimii.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
lähtö:
Lokiaritmeettiset toiminnot
Alla on log-aritmeettiset toiminnot:
1. exp ()
Tämä toiminto laskee eksponentiaalisen tietyn arvon (e x ). On myös muita alatyyppejä, kuten frexp (), Idexp (), joka palauttaa mantissan ja kerrotaan x: n voimaan.
Syntaksi:
return type exp(value);
Esimerkki:
Ohjelma laskee käyttäjän numeerisen arvon eksponentin laskemiseksi annetulle arvolle ja palauttaa kaksinkertaisen arvon.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
ulostulo

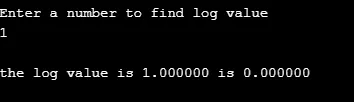
2. loki ()
Tämä toiminto palauttaa tietyn luvun logaritmi-arvon. (kantaan e. loki e )
Syntaksi:
double log(arg);
Esimerkki:
Seuraavassa esimerkissä log-arvo annetulle numerolle lasketaan funktion avulla. Käyttäjän määrittelemä funktio lgm () laskee ja funktiota kutsutaan päätoiminnossa.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
lähtö:
johtopäätös
Yhteenvetona voidaan todeta, että olemme nähneet erilaisia matemaattisia funktioita, joita käytetään C-ohjelmoinnissa, ja nämä ovat suorat kirjaston toiminnot. C-ohjelmat hyödyntävät näitä toimintoja erilaisiin matemaattisiin toimintoihin. Joidenkin monimutkaisten laskentaversioiden ratkaisemiseksi tämä sisäänrakennettu toiminto hyödyttää matemaattisesti suuntautunutta ohjelmointikieltä yksinkertaisten arvojen palauttamiseksi.
Suositellut artikkelit
Tämä on opas matematiikkafunktioihin C. Tässä keskustellaan C: n erilaisista matemaattisista funktioista esimerkkien avulla. Voit myös käydä läpi muiden ehdottamiemme artikkeleidemme -
- PHP-matematiikan toiminnot
- JavaScript-matematiikan toiminnot
- Siirtotoiminnot Matlabissa
- JavaScript-merkkijono-toiminnot
- Johdatus matemaattisiin toimintoihin Pythonissa
- Yleiskatsaus matematiikan toiminnoista C #: ssä
- C Matriisin kertolaskun ohjelmointi
- Neliöjuuri PHP: ssä
- Esimerkkejä JavaScriptin neliöjuurista