Lineaarinen regressio Excelissä - Kuinka tehdä lineaarinen regressio Excelissä?

Lineaarinen regressio Excelissä (sisällysluettelo)

Johdatus lineaariseen regressioon Excelissä
Menetelmät lineaarisen regression käyttämiseksi Excelissä

Johdatus lineaariseen regressioon Excelissä

Lineaarinen regressio on tilastollinen tekniikka / menetelmä, jota käytetään tutkimaan kahden jatkuvan kvantitatiivisen muuttujan välistä suhdetta. Tässä tekniikassa riippumattomia muuttujia käytetään ennustamaan riippuvan muuttujan arvo. Jos on vain yksi riippumaton muuttuja, niin se on yksinkertainen lineaarinen regressio, ja jos joukko riippumattomia muuttujia on enemmän kuin yksi, niin se on useita lineaarisia regressioita. Lineaarisella regressiomallilla on suhde riippuvien ja riippumattomien muuttujien välillä sovittamalla lineaarinen yhtälö havaittuihin tietoihin. Lineaarisella tarkoitetaan sitä, että käytämme riviä sopimaan tietoihimme. Regressioanalyysissä käytettyjä riippuvaisia muuttujia kutsutaan myös vaste- tai ennustetuiksi muuttujiksi, ja riippumattomia muuttujia kutsutaan myös selittäviksi muuttujiksi tai ennustajiksi.

Lineaarisella regressioviivalla on yhtälö: Y = a + bX;

Missä:

X on selittävä muuttuja,
Y on riippuvainen muuttuja,
b on viivan kaltevuus,
a on y-leikkaus (ts. y: n arvo, kun x = 0).

Pienimmän neliösumman menetelmää käytetään yleensä lineaarisessa regressiossa, joka laskee parhaiten sopivan viivan havaittuihin tietoihin minimoimalla datapisteiden poikkeamisen neliöiden summa linjalta.

Menetelmät lineaarisen regression käyttämiseksi Excelissä

Tämä esimerkki opettaa sinulle menetelmiä lineaarisen regression analyysin suorittamiseksi Excelissä. Katsotaanpa joitain menetelmiä.

Voit ladata tämän lineaarisen regression Excel -mallin täältä - Lineaarisen regression Excel -mallin

Menetelmä # 1 - Hajakaavio trendiviivalla

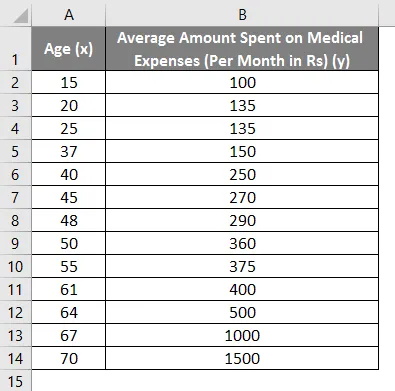
Oletetaan, että meillä on tietojoukko joistakin henkilöistä, joiden ikä, biomassaindeksi (BMI) ja summa, jonka he käyttävät sairauskuluihin kuukaudessa. Nyt saamme käsityksen yksilöiden ominaisuuksista, kuten ikä ja painoindeksi, haluamme selvittää, miten nämä muuttujat vaikuttavat sairaanhoitokuluihin, ja tämän vuoksi käyttää niitä suorittamaan regressiota ja arvioimaan / ennustamaan joidenkin tiettyjen henkilöiden keskimääräisiä sairauskuluja. Katsotaan ensin, kuinka vain ikä vaikuttaa sairauskuluihin. Katsotaanko aineisto:

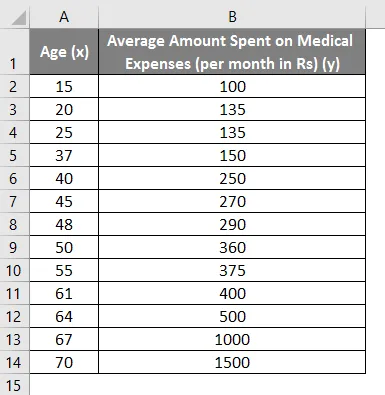
Sairauskulujen määrä = b * ikä + a

Valitse tietojoukon kaksi saraketta (x ja y), mukaan lukien otsikot.

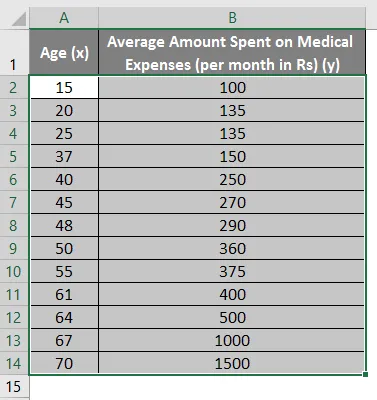
Napsauta 'Lisää' ja laajenna 'Scatter Chart' -valikkoa ja valitse 'Scatter' pikkukuva (ensimmäinen)

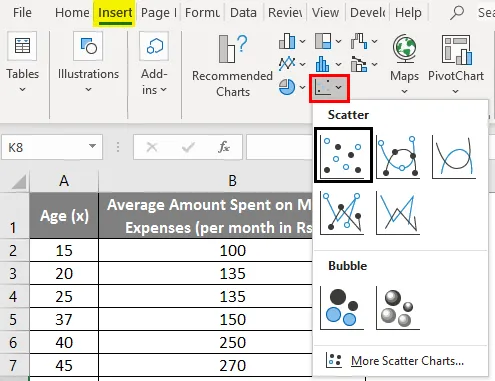
Nyt sirontakaavio ilmestyy, ja piirrämme regressioviivan tähän. Voit tehdä tämän napsauttamalla hiiren kakkospainikkeella mitä tahansa datapistettä ja valitsemalla Lisää trendi

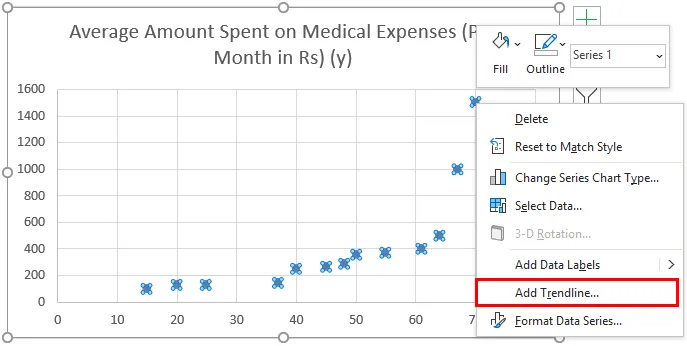
Valitse nyt oikeanpuoleisessa ”Format Trendline” -ikkunassa ”Linear Trendline” ja ”Display Equation on Chart”.

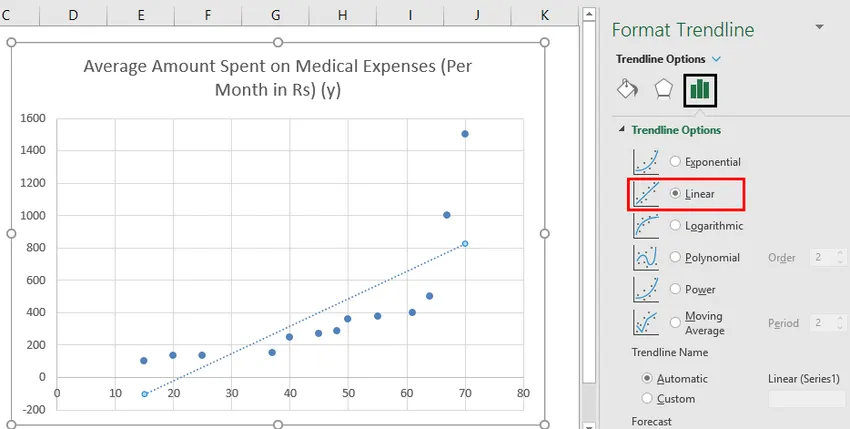
Valitse 'Näytä yhtälö kaaviossa'.

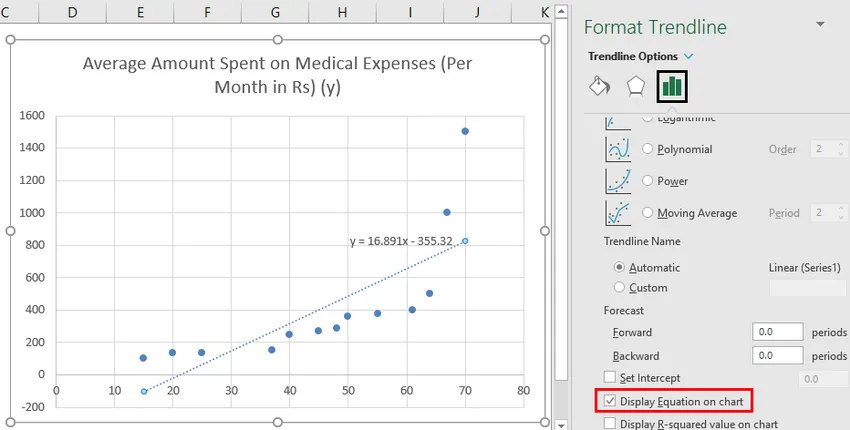
Voimme improvisoida kaavion tarpeidemme mukaan, kuten lisätä akselinimikkeitä, muuttaa mittakaavaa, väriä ja viivatyyppiä.

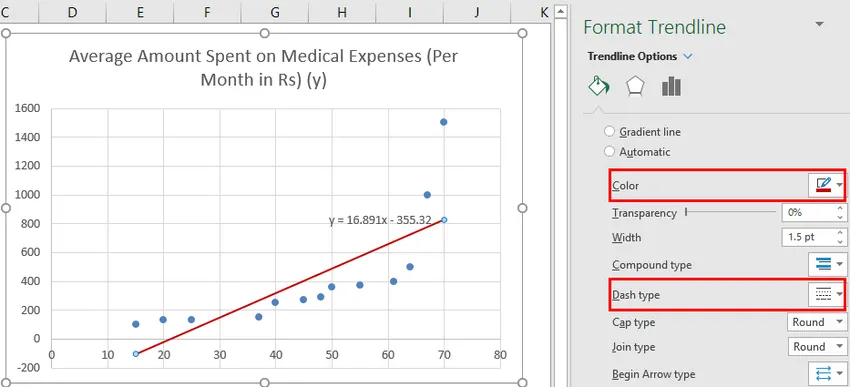
Kaavion parantamisen jälkeen saamme tämän tuloksen.

Huomaa: Tämän tyyppisessä regressiograafissa riippuvaisen muuttujan tulisi aina olla y-akselilla ja riippumaton x-akselilla. Jos kuvaaja piirretään päinvastaisessa järjestyksessä, vaihda joko akselit kaaviossa tai vaihda sarakkeet tietojoukossa.

Menetelmä nro 2 - Analysis ToolPak -apuohjelman menetelmä

Analysis ToolPak ei ole joskus oletusarvoisesti käytössä, ja meidän on tehtävä se manuaalisesti. Tehdä niin:

Napsauta 'File' -valikkoa.

Napsauta sen jälkeen "Asetukset".

Valitse 'Hallitse' -ruudusta 'Excel-lisäosat' ja napsauta 'Siirry'

Valitse 'Analysis ToolPak' -> 'OK'

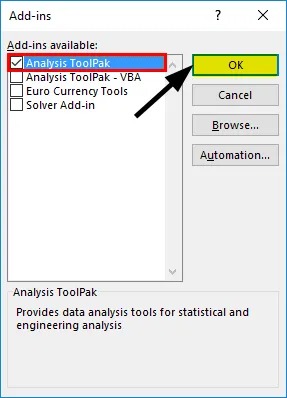
Tämä lisää 'Data Analysis' -työkalut 'Data' -välilehteen. Nyt suoritamme regressioanalyysin:

Napsauta 'Data' -välilehden 'Data Analysis'

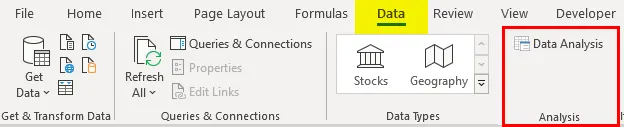
Valitse 'Regressio' -> 'OK'

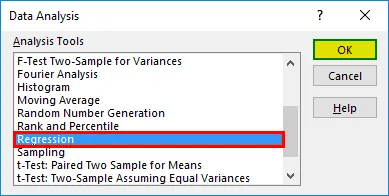
Regressiovalintaikkuna tulee näkyviin. Valitse Input Y -alue ja Input X -alue (sairauskulut ja ikä vastaavasti). Usean lineaarisen regression tapauksessa voimme valita enemmän riippumattomien muuttujien sarakkeita (esimerkiksi jos haluamme nähdä myös BMI: n vaikutuksen sairauskuluihin).
Lisää otsikot valitsemalla Tarrat-ruutu.
Valitse haluamasi lähtö.
Valitse 'jäännökset' -valintaruutu ja napsauta 'OK'.

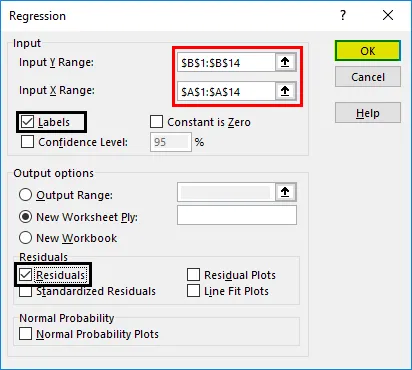
Nyt regressioanalyysituotteemme luodaan uudelle taulukolle, jossa ilmoitetaan regression tilastot, ANOVA, jäännökset ja kertoimet.

Tuloksen tulkinta:

Regressiotilastot kertovat kuinka hyvin regressioyhtälö sopii tietoihin:

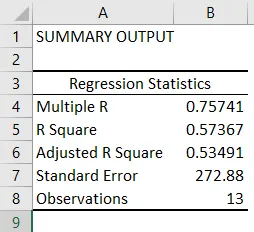
Monikerta R on korrelaatiokerroin, joka mittaa lineaarisen suhteen vahvuutta kahden muuttujan välillä. Se on välillä -1 ja 1, ja sen absoluuttinen arvo kuvaa suhteen voimakkuutta suurella arvolla, joka osoittaa vahvemman suhteen, matala arvo ilmaisee negatiivisen ja nolla arvo, joka osoittaa, ettei suhdetta ole.
R-neliö on määrityskerroin, jota käytetään sopivuuden osoittimena. Se on välillä 0 ja 1, ja arvo lähellä 1 osoittaa, että malli on hyvä istuvuus. Tässä tapauksessa 0, 57 = 57% y-arvoista selitetään x-arvoilla.
Säädetty R-neliö on R-neliö, joka on säädetty ennustajien lukumäärää varten, jos on olemassa useita lineaarisia regressioita.
Vakiovirhe kuvaa regressioanalyysin tarkkuutta.
Havainnot kuvaavat mallimittausten lukumäärää.
Anova kertoo regressiomallin variaatioasteen.

Tätä ei yleensä käytetä yksinkertaiseen lineaariseen regressioon. 'Merkitys F -arvot' osoittavat kuitenkin, kuinka luotettavia tuloksemme ovat, ja arvo, joka on suurempi kuin 0, 05, ehdottaa toisen ennustajan valitsemista.

Kertoimet ovat tärkein osa regressioyhtälön muodostamiseen.

Joten regressioyhtälömme olisi: y = 16, 891 x - 355, 32. Tämä on sama kuin menetelmällä 1 (sirontakaavio trendiviivalla).

Jos nyt haluamme ennustaa keskimääräisiä sairauskuluja, kun ikä on 72 vuotta:

Joten y = 16, 891 * 72 -355, 32 = 860, 832

Joten tällä tavalla voimme ennustaa y-arvot kaikille muille x-arvoille.

Jäännökset osoittavat todellisten ja ennustettujen arvojen eron.

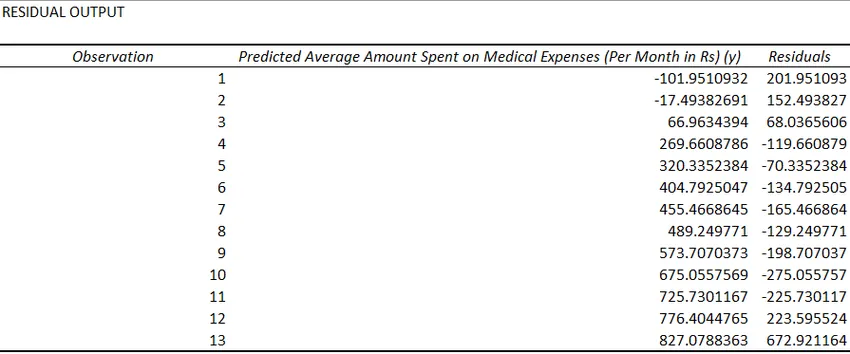
Viimeistä regressiointimenetelmää ei käytetä niin yleisesti ja se vaatii tilastollisia toimintoja, kuten kaltevuus (), sieppaaminen (), korrelointi () jne. Regressioanalyysin suorittamiseksi.

Muistettavat tiedot lineaarisesta regressiosta Excelissä

Regressioanalyysiä käytetään yleensä selvittämään, onko kahden muuttujasarjan välillä tilastollisesti merkitsevä yhteys.
Sitä käytetään ennustamaan riippuvaisen muuttujan arvo yhden tai useamman riippumattoman muuttujan arvojen perusteella.
Aina kun haluamme sovittaa lineaarisen regressiomallin tietoryhmään, data-aluetta tulisi tarkkailla tarkkaan, kuin jos regressioyhtälöä käytetään ennustamaan minkä tahansa arvon tämän alueen ulkopuolella (ekstrapolointi), niin se voi johtaa väärään tulokseen.

Suositellut artikkelit

Tämä on opas Lineaariseen regressioon Excelissä. Tässä keskustellaan siitä, kuinka Lineaarinen regressio tehdään Excelissä, sekä käytännön esimerkkejä ja ladattavaa Excel-mallia. Voit myös käydä läpi muiden ehdottamiemme artikkeleidemme -