3D-matriisi MATLABissa
MATLAB on tekniseen laskentaan käytetty kieli. Kuten suurin osa meistä on samaa mieltä, helppokäyttöinen ympäristö on välttämätön laskennan, visualisoinnin ja lopulta ohjelmoinnin tehtävien integroimiseksi. MATLAB tekee saman tarjoamalla ympäristön, jota ei ole vain helppo käyttää, vaan myös saamme ratkaisut näytetään matemaattisina merkinnöinä, jotka useimmat meistä tuntevat. Tässä aiheessa aiomme oppia 3D-matriisista MATLABissa.
MATLAB-käyttökohteet sisältävät
- laskeminen
- Algoritmien kehittäminen
- mallintaminen
- Simulointi
- prototyyppien
- Data-analytiikka (tietojen analysointi ja visualisointi)
- Suunnittelu ja tieteellinen grafiikka
- Sovellus kehitys
Tässä artikkelissa ymmärretään moniulotteisia matriiseja MATLABissa ja tarkemmin sanottuna kolmiulotteista matriisia Matlabissa.
Moniulotteinen taulukko
Se on MATLAB: n taulukko, jolla on kaksi tai useampi ulottuvuus. Saatat jo tietää, että 2D-matriisin mitat esitetään riveillä ja sarakkeilla.
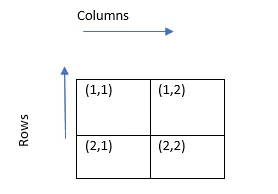
Jokaisella elementillä on kaksi alaindeksiä, joista toinen on rivi-indeksi ja toinen on sarake-indeksi.
Esimerkiksi (1, 1) elementti edustaa tässä Rivinumero on 1 ja sarakkeen numero on 1.
Mikä on 3D-matriisi?
3-D-matriisi on moniulotteinen matriisi, joka on kaksiulotteisen matriisin jatke. Kuten voit arvata, heillä on 3 alaindeksiä, yksi alaindeksi sekä rivi- ja sarakeindeksit kuin 2D-matriisilla. Kolmatta 3D-matriisin alaindeksiä käytetään elementin arkkien tai sivujen esittämiseen.
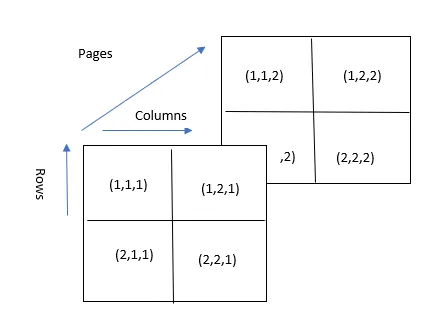
Esimerkiksi tässä elementti (2, 1, 1) edustaa 'Rivi' numero 2 'Sarake' numero yksi ja 'Sivu' numero 1.
3D-matriisin luominen
Ymmärretään nyt, kuinka voimme luoda 3D-matriisin MATLABiin
Kolmiulotteiseen matriisiin luo ensin 2D-matriisi ja laajenna se sitten 3D-matriisiin.
- Luo kolmiulotteinen matriisi kolmiulotteisen matriisin ensimmäisenä sivuna (voit selvästi nähdä, että me luomme ensin 2D-matriisin)
A = (11 2 7; 4 1 0; 7 1 5)
- Lisää toinen sivu nyt. Tämä voidaan tehdä osoittamalla vielä yksi 3: 3-matriisi, jonka indeksi-arvo 2 on kolmannessa ulottuvuudessa
A (:, :, 2) = (1 2 5; 4 4 6; 2 8 1)
A (3 x 3)
A =
| A (:, :, 1) = | 11 | 2 | 7 |
| 4 | 1 | 0 | |
| 7 | 1 | 5 |
| A (:, :, 2) = | 1 | 2 | 5 |
| 4 | 4 | 6 | |
| 2 | 8 | 1 |
Voimme käyttää myös nimeltään cat Function -toimintoa moniulotteisten taulukkojen luomiseen.
Esimerkki: Luo kolmiulotteinen 3D-taulukko kissan avulla
X = kissa (3, A, (3 7 1; 0 1 8; 2 5 4))
- Tässä A on yllä luotu 3D-taulukko
- Argumentti ensimmäisessä paikassa (3) kertoo mihin suuntaan ryhmä on ketjuttava
- Täällä ketjuttaminen tapahtuu sivujen kanssa
X =
| X (:, :, 1) = | 11 | 2 | 7 |
| 4 | 1 | 0 | |
| 7 | 1 | 5 |
| X (:, :, 2) = | 1 | 2 | 3 |
| 4 | 4 | 6 | |
| 2 | 8 | 1 |
| X (:, :, 3) = | 3 | 7 | 1 |
| 0 | 1 | 8 | |
| 2 | 5 | 4 |
Nyt, jos meidän on laajennettava tätä taulukkoa edelleen, voimme yksinkertaisesti antaa 4. taulukon elementit, jotka meidän on lisättävä:
Joten laajentaaksesi yllä olevaa esimerkkiä, annamme yksinkertaisesti,
B (:, :, 4) = (1 2 1; 3 9 1; 6 3 7) ja tulos on:
X =
| X (:, :, 1) = | 11 | 2 | 7 |
| 4 | 1 | 0 | |
| 7 | 1 | 5 |
| X (:, :, 2) = | 1 | 2 | 3 |
| 4 | 4 | 6 | |
| 2 | 8 | 1 |
| X (:, :, 3) = | 3 | 7 | 1 |
| 0 | 1 | 8 | |
| 2 | 5 | 4 |
| X (:, :, 4) = | 1 | 2 | 1 |
| 3 | 9 | 1 | |
| 6 | 3 | 7 |
Kuinka pääsemme taulukon elementteihin?
Käytä tätä varten alaindeksejä kokonaislukuina. Joten 3D-matriisin 2, 3, 1 -elementti on elementti, joka on 2. rivin ensimmäisen sivun 3. sarakkeessa
Käytämme tämän osoittamiseen 3D-matriisia A, jota käytimme yllä,
Nyt pääsy = A (2, 3, 1) antaa meille 0 tulosteena
Toiminnot moniulotteisen taulukon elementtien käsittelemiseksi
MATLAB tarjoaa meille pari toimintoa moniulotteisen taulukon elementtien käsittelemiseksi.
- muokkaamaan
- permute
Ymmärretään nämä yksitellen:
1. Muuta
Tämä on hyödyllistä pääasiassa datan visualisoinnin aikana
Esimerkki: Luo 6 * 5 -matriisi käyttämällä kahta 3 * 5 -matriisia
- A = (1 3 7 0 5; 2 0 4 1 3; 1 0 5 3 2);
- A (:, :, 2) = (1 7 2 5 0; 4 2 1 6 5; 1 1 4 5 0);
- B = muotoilu (A, (6 5))
Tämä luo 2D-matriisin, jossa on 6 riviä ja 5 saraketta:
B = 6 × 5
1 7 5 7 5
2 4 3 2 6
1 5 2 1 5
3 0 1 2 0
0 1 4 1 5
0 3 1 4 0
Kuten huomaat, RESHAPE toimii sarakekohtaisesti, joten ensin kaikki A: n elementit kulkevat ensimmäisen sivun sarakkeessa. Sama asia tehdään sitten 2. sivulle
2. Pysäytä
Voimme käyttää tätä toimintoa, jos haluamme muuttaa matriisien mittoja. eli rivien vaihtaminen sarakkeilla tai päinvastoin.
Esimerkki permutista
- P (:, :, 1) = (3 5 3; 1 5 2; 0 8 5);
- P (:, :, 2) = (0 1 3; 6 7 1; 4 2 1)
Käytämme nyt PERMUTE-toimintoa P: ssä:
- M = permute (P, (2 1 3))
Saadaan tulokseen rivit ja sarakkeet vaihdetaan seuraavasti:
M1 =
| M1 (:, :, 1) = | 3 | 1 | 0 |
| 5 | 5 | 8 | |
| 3 | 2 | 5 |
| P1 (:, :, 2) = | 0 | 6 | 4 |
| 1 | 7 | 2 | |
| 3 | 1 | 1 |
Suositellut artikkelit
Tämä on opas 3D-matriisiin MATLABissa. Tässä keskustellaan MATLAB: n käytöstä, mikä on 3D-matriisi? ja miten luodaan 3D-taulukkoja MATLABiin ja joitain manipulaatioita niihin. Voit myös tarkastella seuraavaa artikkelia saadaksesi lisätietoja -
- Matriisi Matlabissa
- MATLAB-versio
- Vektorit Matlabissa
- Tietotyypit MATLABissa
- Pesän tietotyyppi
- PL / SQL-tietotyypit