Tilakaava - Laskin (esimerkkejä Excel-mallilla)

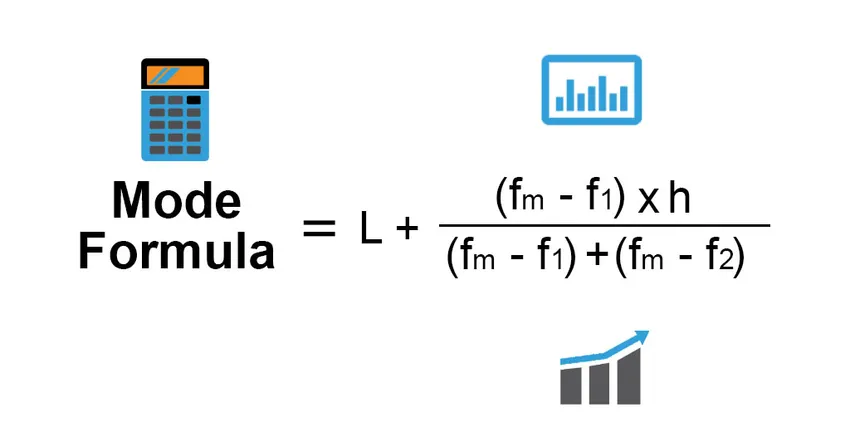
Mode-kaava (sisällysluettelo)

• Kaava
• esimerkit
• Laskin

Mikä on Mode-kaava?

Kolme keskittymismittaa ovat keskimääräinen mediaani ja moodi. Kun kaikkia kolmea käytetään yhdessä erottamaan merkityksellinen analyysi tietojoukosta. Tänään tässä artikkelissa keskustelemme moodista, joka on myös yksi avaimista ja tärkeästä menetelmän keskeisestä taipumuksesta. Tila viittaa tietojoukon yleisimmin esiintyvään arvoon. Datan tila löytyy normaalista tietojoukosta, ryhmädatajoukosta sekä ryhmittelemättömästä tai ryhmittelemättömästä datajoukosta. Keskimääräinen, jota käytetään yleisimmin, on kuitenkin edelleen paras mitta keskitetylle taipumukselle keskiarvon, mediaanin ja moodin olemassaolosta huolimatta. Tässä artikkelissa yritetään ymmärtää moodifunktio, esimerkit ja selitykset jokaisesta esimerkistä yhdessä kaavan ja laskelmien kanssa.

Moodin kaava on: -

Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)

Tilakaava ryhmitetyille tiedoille:

Tila = L + (fm − f1) h / 2fm − f1 − f2

Missä,

• L = modaaliluokan alarajatila
• fm = modaaliluokan taajuus
• f1 = modaaliluokkaa edeltävän luokan taajuus
• f2 = modaaliluokkaa seuraavan luokan taajuus
• h = luokkavälin koko

Esimerkkejä tilakaavasta (Excel-mallilla)

Otetaan esimerkki ymmärtääksesi tilan laskennan paremmin.

Voit ladata tämän Mode Formula Excel -mallin täältä - Mode Formula Excel Template

Tilakaava - esimerkki 1

Missä tila lasketaan yksinkertaisesti havaintomäärät tietojoukossa, joka tapahtuu suurimman osan ajasta.

Laske seuraavan tietojoukon tila.

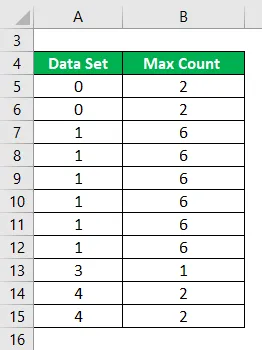
Ratkaisu:

Tila lasketaan seuraavasti:

Havaintojen lukumäärä tietojoukossa, joka esiintyy suurimman osan ajasta

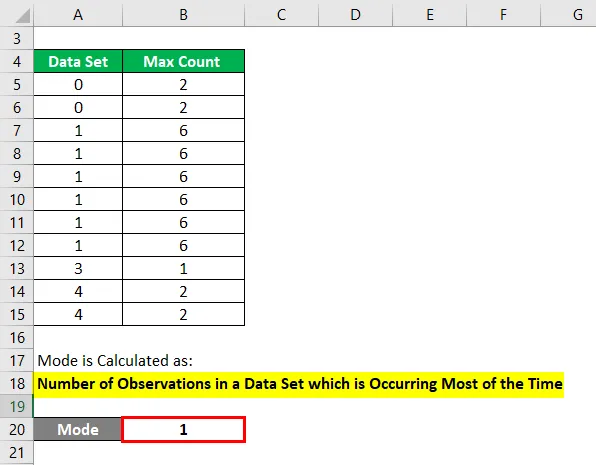
• Tila = 1

Tilakaava - esimerkki 2

Laske tila käyttämällä annettuja tietoja.

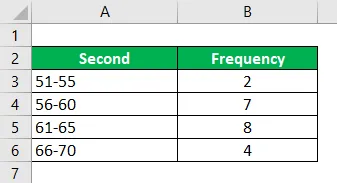
Ratkaisu:

Huomaa: - Ensin on tunnistettava korkeimmalla taajuudella varustettu modaaliryhmä. Jos aikaväli ei ole jatkuva, 0, 5 tulisi vähentää alarajatilasta ja 0, 5 lisätä ylärajatilasta. Silloin väli on

Modaaliryhmä lasketaan seuraavasti:

Modaaliryhmä, joka on yleisin eli 60, 5-65, 5

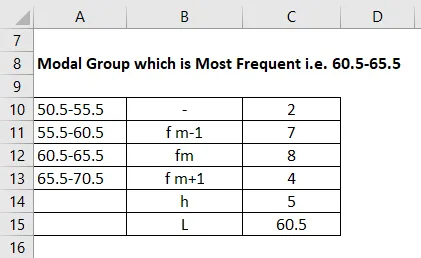
Sitten alempi taajuus on modaaliryhmältä, joka on 4, tässä tapauksessa otetaan fm + 1 ja fm-1 tulee 7 tässä esimerkissä. Ja meillä on fm, joka on taajuus 8. ((h) kutsutaan luokkavälin kokoksi 5, jonka katsomme myös aloitusvälin. L on 60, 5.

Tila lasketaan käyttämällä alla olevaa kaavaa

Tila = L + (fm − f1) h / (fm − f1) + (fm − f2)

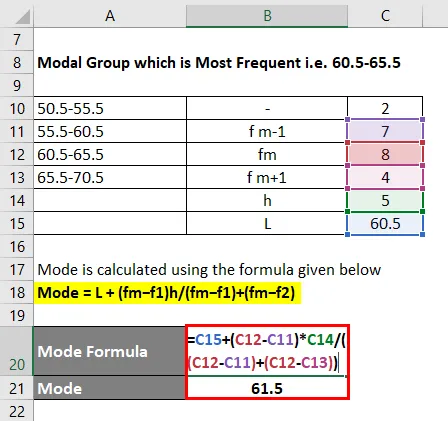
• Tila = 60, 5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
• Tila = 61, 5

Tilakaava - esimerkki 3

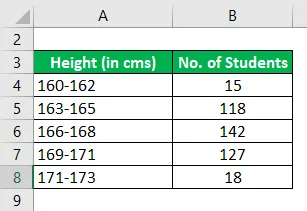
Seuraavat ovat korkeuksien jakaumat tietyssä oppilaiden luokassa tietyssä tilassa

Laske tila käyttämällä annettuja tietoja.

Ratkaisu:

Jos väli ei ole jatkuva, 0, 5 tulisi vähentää alarajatilasta ja 0, 5 lisätä ylärajatilasta. Silloin väli on

Modaaliryhmä lasketaan seuraavasti:

Modaaliryhmä, joka on yleisin eli 165, 5-168, 5

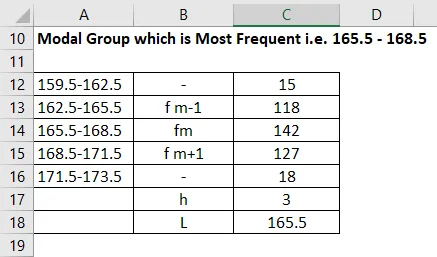
Tila lasketaan alla olevan kaavan avulla

Tila = L + (fm − f1) h / (fm − f1) + (fm − f2)

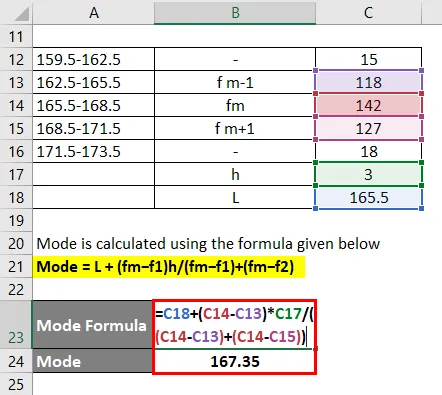
• Tila = 165, 5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
• Tila = 167, 35

Selitys

Tila voidaan selittää yksinkertaisesti arvona, joka esiintyy yleisimmin tietojoukossa. Ja yllä oleva tila voidaan selittää sillä, että kun data on ryhmä, meidän on ensin laskettava modaalifunktio ja tehtävä myös datasta jatkuva, jotta datatila voidaan laskea. Modaaliluokasta päätetään luokalla, jolla on datajoukon korkein taajuus.

Tilakaavan osuvuus ja käyttö

• Keskiarvo, mediaani ja tila paljastavat tietosi eri näkökohdat. Kuka tahansa antaa sinulle yleisen idean, mutta voi johtaa harhaan; Jos sinulla on kaikki kolme, saat täydellisemmän kuvan
• Normaalijakaumaa varten moodilla, keskiarvolla, mediaanilla on sama arvo, koska moodi on normaali jakauma. Analyysitila erikseen ei heijasta todellista kuvaa. Jos haluat analysoida koko tietojoukkoa, kaikki kolme tilastollista mittaa tulisi analysoida yksityiskohtaisesti ja tulkita
• Tila on helppo ymmärtää ja helppo laskea.
• Äärimmäisen suuret tai pienet arvot eivät vaikuta tilaan.
• Tila voidaan löytää vain tarkastelemalla ryhmittelemätöntä dataa ja erillistä taajuuden jakautumista.
• Tila voi olla hyödyllinen laadulliselle tiedolle.
• Tila voidaan laskea avoimen taajuuden taulukossa.
• Tila voi sijaita graafisesti
• Tietotieteilijät käyttävät moodia yleisimmin
• Tila on, että se ei tarjoa meille kovin hyvää keskimääräistä taipumusta, kun yleisin merkki on kaukana muista tietojoukon tiedoista

Mode-kaavolaskin

Voit käyttää seuraavaa moodin kaavalaskuria

L
fm
f1
F2
h
Mode-kaava

Tilakaava =	L + (fm - f1) xh / (fm - f1) + (fm - f2)
=	0 + (0 - 0) x 0 / (0 - 0) + (0 - 0) = 0

Suositellut artikkelit

Tämä on mode-kaavan opas. Tässä keskustellaan siitä, kuinka moodin kaava voidaan laskea yhdessä käytännön esimerkkien kanssa. Tarjoamme myös tilalaskurin ladattavalla excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -

1. Esimerkkejä Gordonin kasvumallikaavasta
2. Kaava pääomavarojen hinnoittelumallin laskemiseen
3. Laskuri kokonaiskulusuhteen kaavalle
4. Poisson Distribution Formula (esimerkkejä Excel-mallilla)