
Ero Z-pisteiden ja T-pisteiden välillä
Z-piste on raakadatan muuntaminen vakiopisteeksi, kun muuntaminen perustuu populaation keskiarvoon ja populaation keskihajontaan. Kun täysi tietojoukko on saatavilla kanssamme, voimme laskea Z-pisteet. Z-piste on väestön keskiarvon vähennys raakapisteestä ja jakaa sitten tulos väestön keskihajonnalla. T-pistearvo on raakadatan muuntaminen standardipisteeksi, kun muuntaminen perustuu näytteen keskiarvoon ja näytteen keskihajontaan. Kun väestötietojoukko ei ole käytettävissä, meidän on poimittava joitain otantatietoja otoksen keskiarvon ja populaation keskihajonnan laskemiseksi.
Z-pistemäärä
Normaalijakaumassa, jossa täydellisiä tietoja on saatavana, se on etäisyys keskiarvosta. Sen kaava on seuraava,
Z= (x-μ)/σ
Missä,
X = yksittäiset raakatiedot
μ = väestön keskiarvo
σ = väestön keskihajonta
T-pistemäärä
T-piste on yksittäisen keskihajonnan vähennys yksittäisestä keskiarvosta ja jaa sitten tulos näytteen keskihajonnalla koko tulos kerrottuna näytteen koosta. Sen kaava on seuraava,
t = ((- μ)/s)*
= näytteen keskiarvo
μ = väestön keskiarvo
s = näytteen keskihajonta
n = näytteen koko
Otetaan esimerkki ymmärtää sama paremmin:
Lehdessä on kolme alajakoa I, II ja III. Olkoon oikein vastattujen opiskelijoiden lukumäärä 25% eli 75% ei pysty vastaamaan siihen oikein. Vastaavasti olkoon 10% ja 20% ihmisistä, jotka ovat vastanneet osioihin II ja III oikein, joten 90% ja 80% ovat kuitenkin löytäneet osiot II ja III. Oletetaan, että näiden kolmen esineen mittaama kyky on sama ja se on normaalisti jakautunut,
Kunkin luokan oppilaan pistemäärä käytetään laskemaan pisteiden keskiarvo, joka on yhtä suuri kuin 50 ja keskihajonta 10. Voimme laskea Z-pistemäärän pisteellä 50 asteikolla (50-50) / 10 = 0
Voimme tulkita, että opiskelijan pistemäärä on 0 etäisyyttä (keskihajontayksikköinä) keskiarvosta, joten opiskelija on saanut keskiarvon.
Jos pistemäärä on 60, Z-pistemäärä on (60-50) / 10 = 1
Voimme tulkita, että opiskelija on saanut keskiarvon ylittävän pisteen - etäisyys yhden standardipoikkeaman keskiarvon yläpuolella.
Head to Head -vertailu Z-pisteet vs. T-pisteet (infografiat)
Alla on 9 parhainta eroa Z-pisteiden ja T-pisteiden välillä 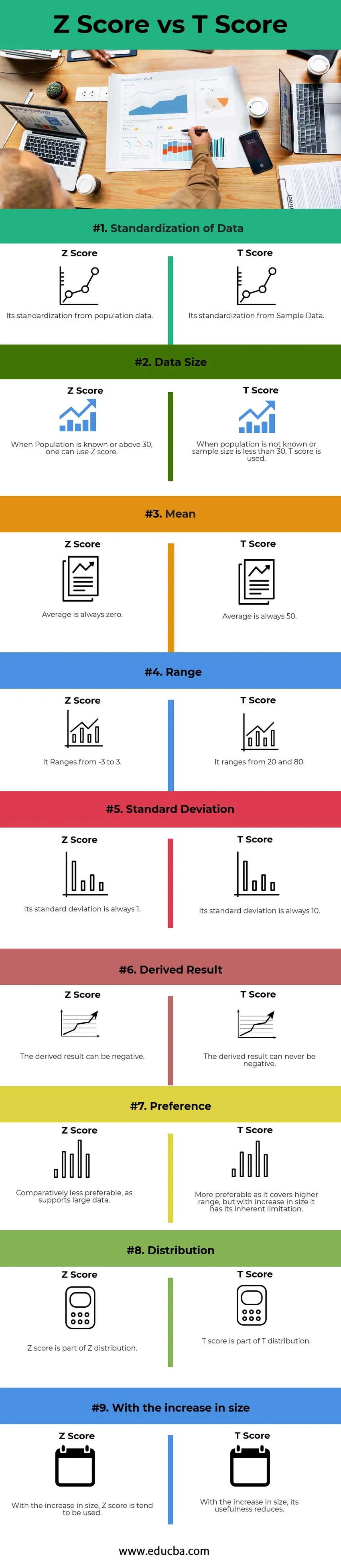
Keskeiset erot Z-pisteet vs. T-pisteet
Keskustelemme joistain suurimmista eroista Z-pisteen vs. T-pisteiden välillä
- Z-pistemäärä on standardointi väestön raakatiedoista tai yli 30 otatiedosta vakioarvoon, kun taas T-pistearvo on standardointi alle 30: n datan näytteetiedoista vakiopisteisiin
- Z-pistemäärä vaihtelee välillä 3 - 3, kun taas T-pistemäärä vaihtelee välillä 20 - 80.
- Kun datan koko kasvaa, jakautumisella on taipumus olla Z-jakaumaa. Sekä Z-pisteet vs. T-pisteet jakautuvat normaalijakaumaan, mutta koon perusteella ne eroavat toisistaan
- Käytännössä Z-pistettä käytetään laajasti osakemarkkinatiedoissa ja yrityksen konkurssiin liittyvien mahdollisuuksien tarkistamiseen, kun taas t-pistettä käytetään laajasti luun mineraalitiheyden ja murtumisriskien arvioinnissa.
Z-pisteen vs. T-pistevertailutaulukko
Katsotaanpa 9 parasta vertailua Z-pisteet vs. T-pisteet
| Sr. Ei | Vertailupisteet | Z pisteytys | T-pistemäärä |
| 1 | Tietojen standardointi | Sen standardointi väestötiedoista | Sen standardointi näytteetiedoista |
| 2 | Tiedon koko | Kun väestö on tiedossa tai yli 30, voidaan käyttää Z-pistemääriä | Jos populaatiota ei tunneta tai näytteen koko on alle 30, käytetään T-pistemäärää. |
| 3 | Tarkoittaa | Keskiarvo on aina nolla. | Keskiarvo on aina 50. |
| 4 | alue | Se vaihtelee välillä -3 - 3. | Se vaihtelee välillä 20 ja 80. |
| 5 | Vakiopoikkeama | Sen keskihajonta on aina 1 | Sen keskihajonta on aina 10 |
| 6 | Johdettu tulos | Johdettu tulos voi olla negatiivinen | Johdettu tulos ei voi koskaan olla negatiivinen |
| 7 | etusija | Suhteellisen vähemmän suositeltava, koska se tukee suurta dataa | Edullisempi, koska se kattaa suuremman alueen, mutta koon kasvaessa sillä on luontainen rajoitus |
| 8 | Jakelu | Z-pistemäärä on osa Z-jakaumaa | T-pistemäärä on osa T-jakaumaa |
| 9 | Koon kasvaessa | Koon kasvaessa Z-pisteytystä käytetään yleensä | Kokon kasvaessa sen hyödyllisyys vähenee. |
johtopäätös
Molemmat Z-pisteet vs. T-pisteet ovat osa hypoteesitestausta normaalin jakauman alla. Jos sinulla on joukko mittauspisteitä eri mittareista Z-pisteitä käyttämällä, voit kertoa, kuinka pisteytys sijoitetaan jakautumiseen. Sitten voit verrata niitä. Pisteiden standardisointi on laajasti käytetty menetelmä tutkimus- ja suunnittelussa, koska ne auttavat vertailla erilaisia testituloksia. Pisteiden standardisointi ennen niiden yhdistämistä auttaa tutkijaa saamaan parempia ja vertailukelpoisempia tuloksia.
Suositellut artikkelit
Tämä on opas Z-pisteet vs. T-pisteiden väliseen eroon. Tässä keskustellaan myös Z-pisteet vs. T-pisteet avaineroista infografien ja vertailutaulukon kanssa. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja-
- Rahoitus vs. taloustiede - suurin ero
- Alijäämä vs. velka - mikä on parempi
- Omaisuuden hankinta vs. osakeosto
- Rahamarkkinat vs. pääomamarkkinat
- Katsaus Altman Z -pisteeseen