
Z-pistekaava (sisällysluettelo)
- Kaava
- esimerkit
- Laskin
Mikä on Z-pisteet?
”Z-pistemäärä” on yksi yleisimmin käytetyistä tilastollisista työkaluista, joita käytetään pisteet standardisoimaan edellyttäen, että populaatio tarkoittaa ja keskihajonta tunnetaan. Sinänsä Z-pistemäärä tunnetaan myös standardipisteenä. Z-pistemäärä vaihtelee välillä -3-kertainen keskihajonta +3-kertaiseksi keskihajontaan keskiarvon ollessa nolla ja keskihajonta yksi. Muuttujan Z-pisteen kaava voidaan johtaa laskemalla väestön keskiarvo annetusta muuttujasta (joka on osa tietojoukkoa tai populaatiota) ja jakamalla sitten tulos populaation keskihajonnalla. Matemaattisesti se esitetään
Z = (X – μ) / σ
missä,
- X = vaihtelee populaatiosta
- μ = väestön keskiarvo
- σ = populaation keskihajonta
Esimerkkejä Z-pisteet-kaavasta (Excel-mallilla)
Otetaan esimerkki ymmärtää Z-pisteen laskeminen paremmin.
Voit ladata tämän Z Score Formula Excel -mallin tästä - Z Score Formula Excel TemplateZ-pistekaava - esimerkki # 1
Otetaan esimerkki Mannystä, joka vastikään ilmestyi SAT: iin. Hän onnistui pisteet 1109 tässä yrityksessä. Saatavilla olevien tietojen mukaan SAT: n keskimääräinen pistemäärä pysyi kuitenkin noin 1030: n tasolla standardipoikkeaman ollessa 250. Laske Mannyn SAT-pisteiden Z-pistemäärä ja arvioi, kuinka hyvin hän menestyi verrattuna keskimääräisiin testinottajiin.
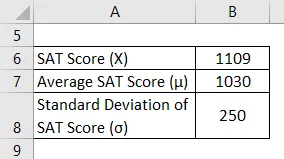
Ratkaisu:
Z Piste lasketaan alla olevan kaavan avulla
Z = (X - μ) / σ
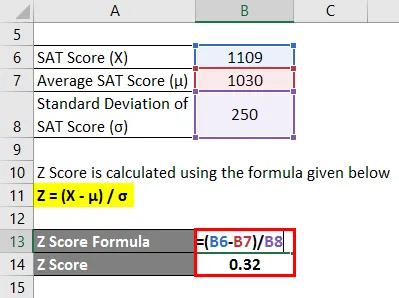
- Z-pisteytys = (1109 - 1030) / 250
- Z-pisteet = 0, 32
Siksi Mannyn SAT-pistemäärä on 0, 32 keskihajontaa korkeampi kuin keskimääräiset testinottajien pisteet, mikä osoittaa, että 62, 55% koehenkilöistä antoi vähemmän pisteitä kuin Manny.
Z-pistekaava - esimerkki 2
Otetaan nyt esimerkki Chelseasta, joka on kirjoittanut SAT: n kahdesti ja haluaa vertailla esitystään heissä. Hän onnistui pisteet 1085 ja 1059 ensimmäisessä ja toisessa yrityksessä. Saatavilla olevien tietojen mukaan keskimääräinen pistemäärä ja keskihajonta olivat ensimmäisessä yrityksessä vastaavasti 1100 ja 230, kun taas jälkimmäisessä se oli 1050 ja 240. Auta Chelseaa päättämään, missä kokeessa hän suoritti paremmin.
Ratkaisu:
Ensimmäinen yritys
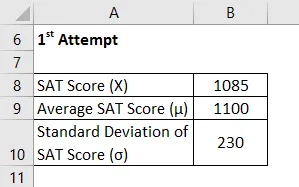
Z Piste lasketaan alla olevan kaavan avulla
Z = (X - μ) / σ
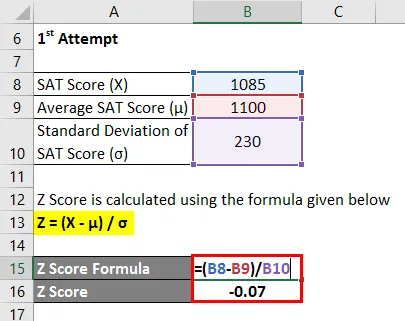
- Z-pisteytys = (1085 - 1100) / 230
- Z-pisteytys = -0, 07
Siksi Chelsean SAT-pistemäärä ensimmäisessä yrityksessä on 0, 07 standardipoikkeamaa pienempi kuin keskimääräinen testinottajien pistemäärä, mikä osoittaa, että 47, 40% testinottajista antoi vähemmän pisteitä kuin Chelsea ensimmäisen yrityksen aikana.
2. yritys
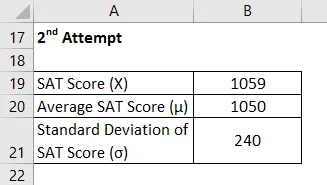
Z Piste lasketaan alla olevan kaavan avulla
Z = (X - μ) / σ
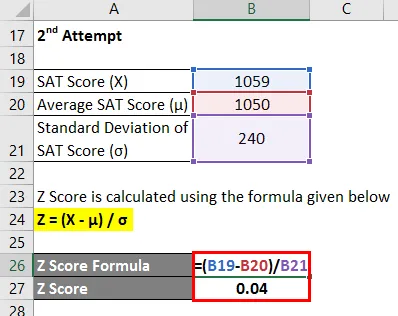
- Z-pisteytys = (1059 - 1050) / 240
- Z-pisteet = 0, 04
Siksi Chelsean SAT-pistemäärä toisessa yrityksessä on 0, 04 keskihajontaa korkeampi kuin keskimääräiset testinottajien pisteet, mikä osoittaa, että 51, 50% testinottajista sai toisen testin aikana vähemmän kuin Chelsea.
Joten Z-pisteiden vertailusta on selvää, että Chelsea menestyi paremmin toisen kerran.
Selitys
Z-pisteen kaava voidaan johtaa seuraavien vaiheiden avulla:
Vaihe 1: Ensin rakennetaan populaatio, jolla on suuri määrä muuttujia, ja muuttujia merkitään X i: llä .
Vaihe 2: Seuraavaksi lasketaan muuttujien lukumäärä populaatiossa ja se merkitään N: llä.
Vaihe 3: Seuraavaksi lasketaan populaation keskiarvo summaamalla kaikki muuttujat, mitä seuraa jakaminen muuttujien kokonaismäärällä (vaihe 2) tietojoukossa. Väestön keskiarvo on merkitty μ.
μ = ∑ X i / N
Vaihe 4: Seuraavaksi vähennä keskiarvo jokaisesta tietojoukon muuttujasta laskemaan niiden poikkeama keskiarvosta.
eli (X i - μ) on i: nnen datapisteen poikkeama.
Vaihe 5: Laske seuraavaksi muuttujien neliöpoikkeamat eli (X i - μ) 2 .
Vaihe 6: Seuraavaksi lasketaan yhteen kaikki neliöpoikkeamat ja jaetaan sitten kokonaisarvo tietojoukon muuttujien määrällä varianssin saavuttamiseksi.
σ 2 = ∑ (Xi - μ) 2 / N
Vaihe 7: Seuraavaksi lasketaan populaation keskihajonta laskemalla edellä olevassa vaiheessa lasketun varianssin neliöjuuri.
σ = √ ∑ (Xi - μ) 2 / N
Vaihe 8: Lopuksi johdetaan Z-pisteen kaava vähentämällä populaation keskiarvo (vaihe 3) muuttujasta ja jakamalla sitten tulos populaation keskihajonnalla (vaihe 7), kuten alla on esitetty.
Z = (X - μ) / σ
Z-pisteet-kaavan merkitys ja käyttö
Tilastotieteilijän kannalta Z-pisteen käsite on erittäin tärkeä, koska se on hyödyllinen määritettäessä todennäköisyys tapahtumaan tapahtuuko normaalin jakauman sisällä vai ei. Itse asiassa Z-pistettä käytetään myös vertailemaan kahta raakapistettä kahdesta eri normaalijakaumasta, ja se tehdään muuntamalla raa'at pisteet Z-pisteiksi tai standardoiduiksi pisteet. Lisäksi positiivinen Z-piste merkitsee keskiarvoa korkeampaa pistemäärää, kun taas negatiivinen Z-pistemäärä tarkoittaa keskimääräistä pienempää pistettä.
Z Pistekaavolaskin
Voit käyttää seuraavaa Z Score Formula Calculator -sovellusta
| X | |
| μ | |
| σ | |
| Z | |
| Z = |
|
|
Suositellut artikkelit
Tämä on opas Z Score Formulaan. Tässä keskustellaan kuinka lasketaan Z-pistemäärä käytännön esimerkkien avulla. Tarjoamme myös Z Score -laskurin ladattavalla excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Esimerkkejä näytteen kokokaavasta
- Kuinka laskea painotettu keskiarvo?
- Korrelaatiokaavan laskin
- Kaava normaalijakauman laskemiseksi
- Esimerkkejä Altman Z -pisteistä