Johdanto hierarkkiseen klusterointialgoritmiin
Hierarkkinen klusterointialgoritmi on valvomaton koneoppimistekniikka. Sen tavoitteena on löytää luonnollinen ryhmittely tietojen ominaisuuksien perusteella.
Hierarkkisen klusterointialgoritmin tavoitteena on löytää sisäkkäiset dataryhmät rakentamalla hierarkia. Se on samanlainen kuin kasvi- tai eläinkunnan biologinen taksonomia. Hierarkkiset klusterit esitetään yleensä käyttämällä dendrogrammin tunnettua hierarkkista puuta.
Hierarkkisen ryhmittelyalgoritmin tyypit
Hierarkkisia klusterointialgoritmeja on 2 tyyppiä:
- eripuraisuutta aiheuttava
- agglomeratiivinen
1. Erottava
Tämä on ylhäältä alas suuntautuva lähestymistapa, jossa se aluksi pitää koko dataa yhtenä ryhmänä ja sitten jakaa sen iteratiivisesti alaryhmiin. Jos hierarkkisen klusterointialgoritmin lukumäärä tunnetaan, jakamisprosessi pysähtyy, kun klusterien lukumäärä on saavutettu. Muu, prosessi pysähtyy, kun dataa ei voida enää jakaa, mikä tarkoittaa, että nykyisestä iteroinnista saatu alaryhmä on sama kuin edellisestä iteraatiosta saatu alaryhmä (voidaan myös katsoa, että jako loppuu, kun jokainen datapiste on klusteri ).
2. Agglomeratiivinen
Se on alhaalta ylöspäin suuntautuva lähestymistapa, joka perustuu klusterien yhdistämiseen. Aluksi data jaetaan m singleton klusteriin (missä m arvo on näytteiden / datapisteiden lukumäärä). Kaksi klusteria yhdistetään yhdeksi iteratiivisesti vähentäen siten klusterien lukumäärää jokaisessa iteraatiossa. Tämä klusterien yhdistämisprosessi pysähtyy, kun kaikki klusterit on sulautettu yhteen tai saavutetaan haluttujen klusterien lukumäärä.
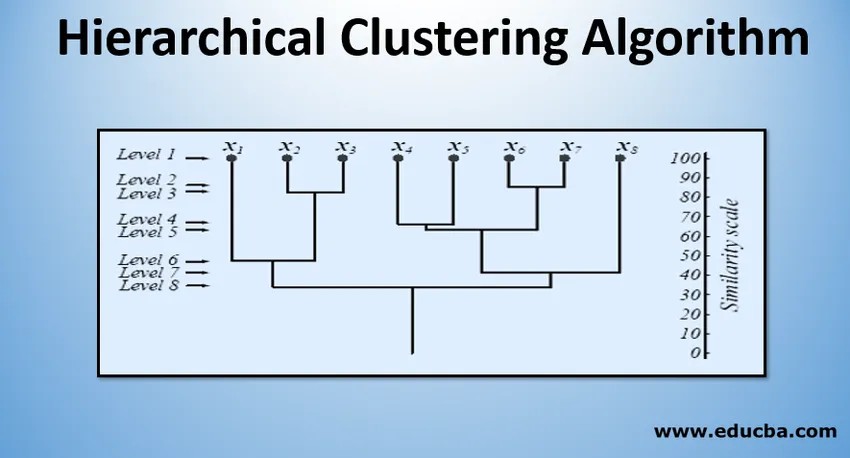
Tasolla 1 on m klusteria, jotka pienenevät yhdeksi klusteriksi tasolla m. Ne tietopisteet, jotka sulautuvat muodostamaan klusterin alemmalla tasolla, pysyvät samassa klusterissa myös korkeimmilla tasoilla. Oletetaan esimerkiksi, että pisteitä x1..x8 on 8, joten aluksi tasolla 8 on 8 klusteria. Oletetaan, että pisteet x1 ja x2 sulautuvat klusteriin tasolla 2, kunnes tasolle 8 ne pysyvät samassa klusterissa.
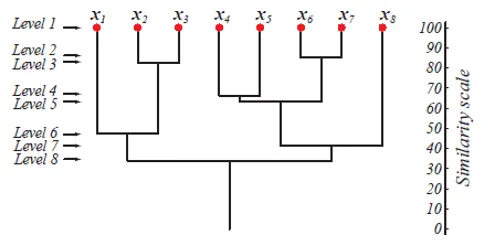
Yllä oleva kuva näyttää dendrogrammaesityksen taajaamon klusterointimenetelmästä 8 datapisteessä sekä kutakin tasoa vastaava samankaltaisuusasteikko.
Klusteritasot antavat meille kuvan siitä, kuinka samankaltaiset klusterien datapisteet ovat. Kuten kuvassa 1 esitetään, aikaisemmin datapisteet sulautuvat klusteriin, samanlaisia kuin ne ovat. Joten klusterin tietopisteet tasolla 2 (esim. X2 ja x3) ovat samankaltaisempia kuin klusterin tason 6 datapisteet (esim. X1 ja x2).
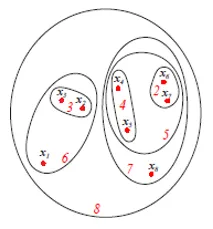
Yllä oleva kuva esittää Set- tai Venn-kaavioesityksen yllä mainittujen 8 datapisteen agglomeratiivisesta klusterointimenetelmästä. Sekä dendrogrammeja että joukkoesityksiä voidaan käyttää klusterointiin. Dendrogrammi on kuitenkin yleensä edullinen omaisuuden esitys, joka ei voi kvantitatiivisesti edustaa klusterien yhtäläisyyksiä.
Hierarkkisen klusteroinnin algoritmin vaiheet
Seuraakaamme seuraavia hierarkkisen klusterointialgoritmin vaiheita:
1. Algoritmi
Agglomeratiivinen hierarkkinen klusterointialgoritmi
- Aloita alustaminen c, c1 = n, Di = (xi), i = 1, …, n '
- Tee c1 = c1 - 1
- Löydä lähimmät klusterit, esimerkiksi Di ja Dj
- Yhdistä Di ja Dj
- Kunnes c = c1
- Palauta c-klusterit
- pää
Tämä algoritmi alkaa n klusterilla, joissa kukin datapiste on klusteri. Jokaisella iteraatiolla klusterien lukumäärä vähenee yhdellä, kun 2 lähintä klusteria sulautuvat yhteen. Tämä prosessi jatkuu, kunnes klusterien lukumäärä vähenee ennalta määritettyyn arvoon c.
Kuinka päättää, mitkä klusterit ovat lähellä?
Se määritetään käyttämällä useita etäisyysmittareita, jotka ovat seuraavat:
- Ryhmien välinen pienin etäisyys dmin (Di, Dj). Hyödyllinen sinkulle.
- Ryhmien välinen suurin etäisyys dmax (Di, Dj). Hyödyllinen kokonaan.
- Keskimääräinen etäisyys klustereiden välillä davg (Di, Dj).
Mikä on yksittäinen kytkentä ja täydellinen kytkentä?
- Kun dmin: tä (di, dj) käytetään kahden klusterin välisen etäisyyden löytämiseen ja algoritmi päättyy, jos lähimpien klusterien välinen etäisyys ylittää kynnyksen, algoritmia kutsutaan yhdeksi kytkentäalgoritmiksi.
- Kun dmax: tä (Di, Dj) käytetään kahden klusterin välisen etäisyyden löytämiseen ja algoritmi päättyy, jos lähimpien klusterien välinen etäisyys ylittää kynnyksen, niin algoritmia kutsutaan täydelliseksi kytkentäalgoritmiksi.
- Tarkastellaan jokaista datapistettä kuvaajan solmuna. Kahden datapisteen välillä on reuna, jos ne kuuluvat samaan klusteriin. Kun kaksi lähintä klusteria yhdistetään, reuna lisätään. Sitä kutsutaan yhdeksi linkkeeksi, koska solmujen välillä on ainutlaatuinen polku.
- Täydellinen kytkentäalgoritmi yhdistää kaksi klusteria minimoimalla etäisyyden kahden kauimman pisteen välillä.
- Yksi kytkentäalgoritmi generoi kattavan puun. Tämä algoritmi on kuitenkin herkkä melulle. Täydellinen kytkentäalgoritmi tuottaa täydellisen kuvaajan.
Mikä on algoritmin aikakompleksiisuus?
Oletetaan, että meillä on n mallia d-ulotteisessa tilassa ja käytämme dmin (Di, Dj) c-klusterien muodostamiseen. Meidän on laskettava n (n - 1) pisteiden välinen etäisyys - jokainen on O (d 2 ) -laskelma - ja sijoitettava tulokset pisteiden väliseen etäisyystaulukkoon. Avaruuden monimutkaisuus on O (n 2 ). Pienimmän etäisyysparin löytäminen (ensimmäistä yhdistämistä varten) edellyttää, että siirrymme läpi täydellisen luettelon pitämällä pienimmän etäisyyden indeksi.
Siten ensimmäisessä agglomeratiivisessa vaiheessa kompleksisuus on O (n (n - 1) (d2 + 1)) = O (n 2 d2). Toista mielivaltaista taajamisvaihetta varten (ts. C1: stä c1 - 1: een), siirrymme vain luettelossa olevien n (n - 1) - c1 "käyttämättömien" etäisyyksien läpi ja löydämme pienimmän, jolle x ja x 'sijaitsevat eri klustereissa. . Tämä on jälleen kerran O (n (n − 1) − c1). Kokonaisajan monimutkaisuus on siten O (cn 2 d 2 ), ja tyypillisissä olosuhteissa n >> c.
2. Visualisointi
Kun tiedot on jaettu klustereihin, on hyvä käytäntö visualisoida klusterit saadaksesi kuvan siitä, miltä ryhmittely näyttää. Mutta tämän korkean ulottuvuuden datan visualisointi on vaikeaa. Siksi käytämme pääkomponenttianalyysiä (PCA) visualisointiin. PCA: n jälkeen saamme datapisteet matalasta ulottuvuudesta (yleensä 2D tai 3D), jotka voimme piirtää nähdäksesi ryhmittelyn.
Huomaa: korkea ulottuvuus tarkoittaa suurta määrää ominaisuuksia eikä useita datapisteitä.3. Arviointi
Yksi klustereiden arviointimenetelmistä on, että klustereiden pisteiden etäisyyden (klusterien välinen etäisyys) tulisi olla paljon enemmän kuin klusterissa olevien pisteiden etäisyys (klusterin sisäinen etäisyys).
johtopäätös
Seuraavassa on muutamia tärkeitä otteita:
- Hierarkkista klusterointialgoritmia käytetään sisäkkäisten kuvioiden löytämiseen tiedoista
- Hierarkkinen klusterointi on 2 tyyppiä - jakavaa ja agglomeratiivista
- Dendrogrammia ja set / Venn-kaaviota voidaan käyttää esittämiseen
- Yksi kytkentä yhdistää kaksi klusteria minimoimalla niiden välisen minimietäisyyden. Se muodostaa kattavan
- Täydellinen linkitys yhdistää kaksi klusteria minimoimalla suurimman etäisyyden. Se muodostaa täydellisen kuvaajan.
- Hierarkkisen klusterointialgoritmin kokonaiskeskeisyys on O (cn 2 d 2 ), missä c on ennalta määrätty klustereiden lukumäärä, n on kuvioiden lukumäärä ja d on n kuvion d-ulotteinen avaruus.
Suositellut artikkelit
Tämä on opas Hierarkkiseen klusterointialgoritmiin. Tässä keskustellaan hierarkkisten klusterointialgoritmien tyypeistä ja vaiheista. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja-
- Hierarkkinen klusterointianalyysi
- Hierarkkinen ryhmittely R ': ssä
- Rypytysalgoritmi
- Mikä on klusterointi tietojen louhinnassa?
- Hierarkkinen ryhmittely | Agglomeratiivinen ja jakautuva klusterointi
- C ++ -algoritmi | Esimerkkejä C ++ -algoritmista