
Keskimääräinen kaava (sisällysluettelo)
- Kaava
- esimerkit
- Laskin
Mikä on keskimääräinen kaava?
Keskiarvo on termi, jota kuulimme tilastoissa ja matemaatikkona tilastollisen keskiarvon nimeltä Keskiarvo. Keskiarvolla on erittäin tärkeä rooli tilastoissa, jos joku haluaa tietää käytettävissä olevan tiedon keskiarvon, jota he voivat käyttää funktion keskiarvona. Excelissä voimme myös helposti selvittää keskiarvon tai keskiarvon tarpeidemme mukaan. Keskiarvo on tilastotermi. Yksinkertaisella termillä voidaan sanoa, että keskiarvo on yksittäinen luku käytettävissä olevan luettelon edustajana. Useat tutkijat käyttävät keskiarvoa tutkimusta tehdessään. Mutta pääasiassa teknisen analyytikon käyttämä keskiarvo, koska heidän on laskettava sen tutkimuksen kohteena olevan kaluston keskimääräinen hinta, joten heillä on keskimäärin enemmän merkitystä omalla alallaan. Keskiarvo on tietojen keskimmäinen luku.
Keskiarvo -
Average = Total Sum of All Numbers / Number of Item in the Set
Esimerkkejä keskimääräisestä kaavasta (Excel-mallilla)
Otetaan esimerkki ymmärtää keskimääräisen kaavan laskenta paremmin.
Voit ladata tämän keskimääräisen Excel-mallin täältä - keskimääräisen Excel-mallinKeskimääräinen kaava - esimerkki 1
Käytettävissä olevat tiedot työvoiman ansaitsemista palkoista viimeisen 4 viikon aikana. Laske työvoiman ansaitsemat keskimääräiset palkat.
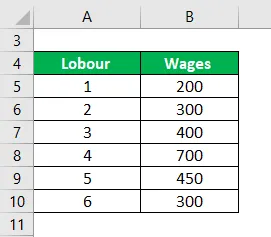
Ratkaisu:
Kaikkien lukujen summa lasketaan seuraavasti:
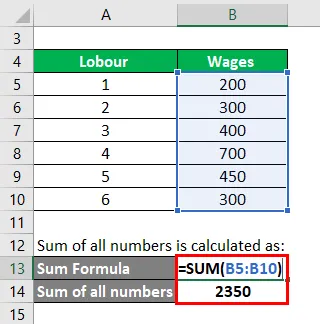
- Kaikkien lukujen summa = 200 + 300 + 400 + 700 + 450 + 3000
- Kaikkien lukujen summa = 2350
Keskiarvo lasketaan alla olevan kaavan avulla
Keskiarvo = Sarjan kaikkien numeroiden / tuotemäärän kokonaissumma
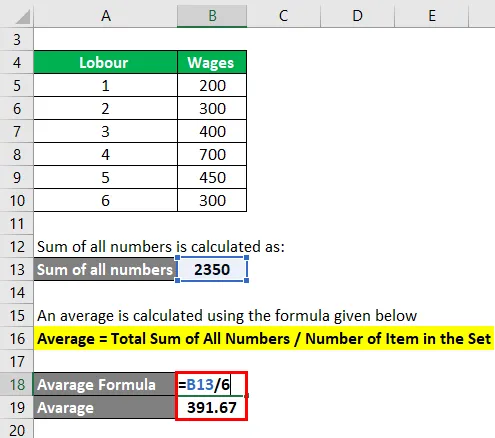
- Keskiarvo = 2350/6
- Keskiarvo = 391, 67
Keskimääräinen kaava - esimerkki 2
Tietoja on saatavilla jäätelön myyntikuukaudesta. Laske saatavilla olevien tietojen perusteella jäätelön keskimääräinen myynti.
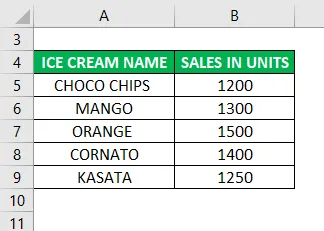
Ratkaisu:
Kaikkien lukujen summa lasketaan seuraavasti:
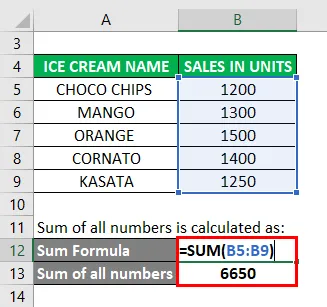
- Kaikkien lukujen summa = 1200 + 1300 + 1500 + 1400 + 1250
- Kaikkien lukujen summa = 6650
Keskiarvo lasketaan alla olevan kaavan avulla
Keskiarvo = Sarjan kaikkien numeroiden / tuotemäärän kokonaissumma
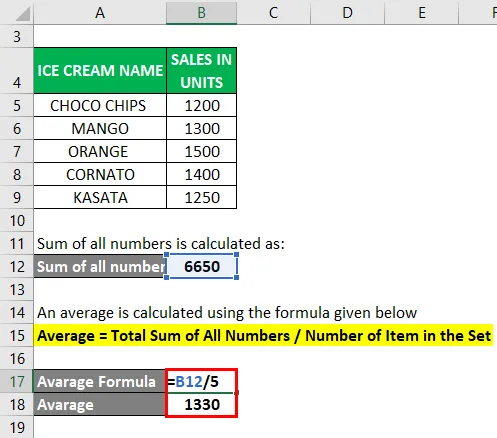
- Keskiarvo = 6650/5
- Keskiarvo = 1330
Keskimääräinen kaava - esimerkki 3
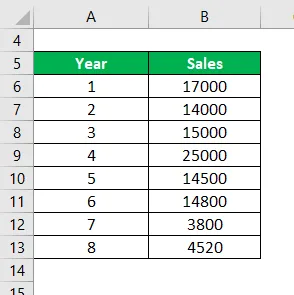
Raymond on tekstiiliyritys ja joka vuosi 100000 erityyppistä kangasta valmistava yritys, joka myy jälleenmyyjälle. Joten yritys haluaa tietää keskimääräisen kuukausimyynnin. Laske käytettävissä olevien tietojen perusteella keskimääräinen myynti.
Ratkaisu:
Kaikkien lukujen summa lasketaan seuraavasti:
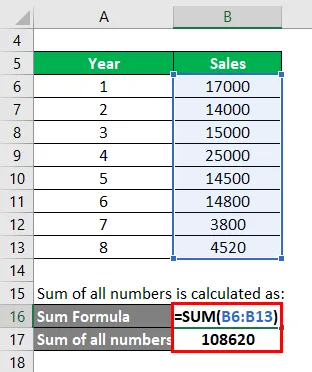
- Kaikkien numeroiden summa = 17000 + 14000 + 15000 + 25000 + 14500 + 14800 + 3800 + 4520
- Kaikkien lukujen summa = 108620
Keskiarvo lasketaan alla olevan kaavan avulla
Keskiarvo = Sarjan kaikkien numeroiden / tuotemäärän kokonaissumma
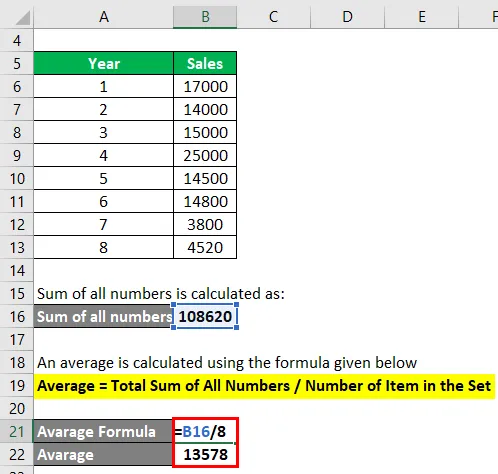
- Keskiarvo = 108620/8
- Keskiarvo = 135778
Keskimääräinen kaava - esimerkki 4
Voltas harjoittaa vaihtovirtalaitteiden valmistusta ja heillä on kumppanuus Youngster Company Limitedin kanssa tuotteensa myymiseksi. He myyvät kuukausittain jälleenmyyjälle 25000 määrää. Joten yrityksen volttit haluavat tietää heidän kokonaismyyntinsä, koska heidän on maksettava jälleenmyyjille palkkiot tuotteen myymisestä. Laske käytettävissä olevien tietojen perusteella yrityksen keskimääräinen myynti.
Ratkaisu:
Kaikkien lukujen summa lasketaan seuraavasti:
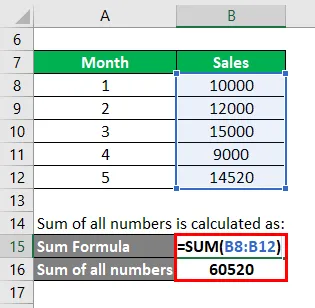
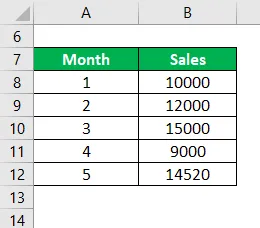
- Kaikkien numeroiden summa = 10000 + 12000 + 15000 + 9000 + 14520
- Kaikkien lukujen summa = 60520
Keskiarvo lasketaan alla olevan kaavan avulla
Keskiarvo = Sarjan kaikkien numeroiden / tuotemäärän kokonaissumma
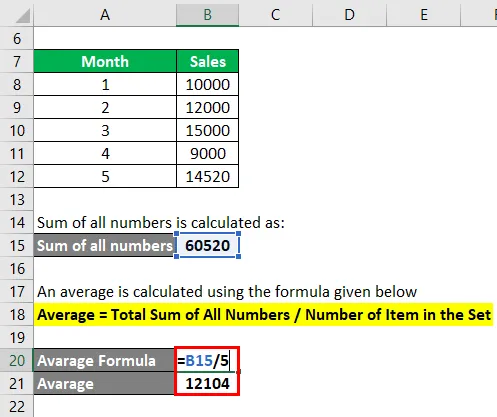
- Keskiarvo = 60520/5
- Keskiarvo = 12104
Kuukausien keskimääräinen myynti on 12104.
Selitys
Keskiarvo on keskeinen luku tiedossa, jota käytetään vastaamaan monen tyyppisiin kysymyksiin ja epäilyihin. Monet ihmiset tutustuivat keskiarvoon jakamalla summan kokonaismäärä kahdella, mutta se ei anna oikeaa lukua. Keskimääräinen kaava ottaen huomioon kaikkien tietojoukossa annettujen lukujen kokonaissumma ja summa jaettuna sarjan alkioiden kokonaismäärällä. Joten keskiarvoa käytetään monin tavoin tietosarjan keskiarvon tuntemiseksi. Yleisellä aikavälillä lasketaan keskiarvo, mutta tilastoissa lasketaan aritmeettinen keskiarvo. Aritmeettinen tarkoittaa myös maallikon kielellä keskimäärin tunnettua. Keskimääräinen voidaan laskea eri tarkoituksiin, sisältää kuukauden keskimääräisen myynnin, keskimääräinen liikevaihto. Se voidaan laskea joko numeron, sarjan, datan, alueen mukaan.
Keskimääräisen kaavan relevanssi ja käyttö
- Tilastoissa tutkija käyttää keskiarvoa löytämiseen.
- Monet yritykset ja organisaatiot käyttävät keskiarvoa selvittääkseen tuotteen keskimääräisen myynnin ja keskimääräisen valmistuksen sekä työntekijöille ja työntekijöille maksettavan keskipalkan.
- WHO (Maailman terveysjärjestö) käytti myös keskiarvoa vuosittaisten kuolemien ja syntyvyyden tietyn ajanjakson aikana.
- Keskiarvo on yksi tärkeimmistä termeistä tilastojen alalla.
- Monien virastojen käyttämä keskiarvo, pohjimmiltaan tietoon käytettävissä olevien tietojen keskinumero tai tiedot.
- Keskiarvo on erittäin tärkeä työkalu tutkimusyrityksen alalla tietyn osakekannan keskimääräisen kaupan hinnan tuntemiseen.
- Keskimääräisellä on erittäin tärkeä rooli osakemarkkinoilla. Monet sijoittajat käyttivät uuden sijoituksen tekemiseen keskimäärin viime vuoden osakekantaa.
- Monentyyppiset laitosorganisaatiot ja sektorit käyttivät keskimäärin vaatimuksiaan ja tarpeitaan kohti.
- Keskimääräinen, jolla on merkitystä kaikilla aloilla ja aloilla, etenkin osakemarkkinoilla, koska analyytikko käyttää niitä usein.
Keskimääräinen kaavolaskin
Voit käyttää seuraavaa keskimääräistä laskinta
| Kaikkien numeroiden kokonaissumma | |
| Sarjan tuotenumero | |
| Keskimääräinen kaava | |
| Keskimääräinen kaava | = |
|
|
Suositellut artikkelit
Tämä on opas keskimääräiseen kaavaan. Tässä keskustellaan kuinka lasketaan keskiarvo yhdessä käytännön esimerkkien kanssa. Tarjoamme myös keskimääräisen laskurin ladattavalla Excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Kuinka laskea korkokulut?
- Vakavaraisuusasteen kaava
- Opas Gordonin kasvumallikaavaan
- Nettovelkakaavan laskeminen