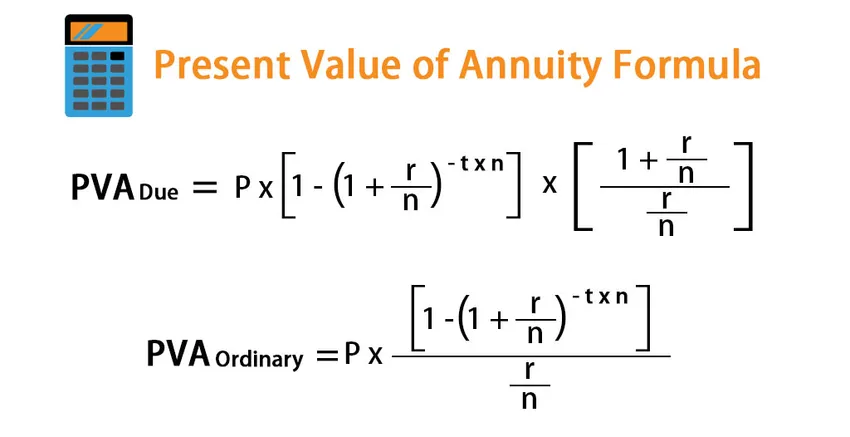
Eläkevakuuden nykyarvo (sisällysluettelo)
- Kaava
- esimerkit
- Laskin
Mikä on elinkorkokaavan nykyarvo?
Termi ”annuiteetin nykyarvo” viittaa samansuuruisten tulevaisuuden maksujen sarjaan, jotka diskontataan nykypäivään. Maksu voidaan kuitenkin vastaanottaa joko kunkin ajanjakson alussa tai lopussa, ja siten on olemassa kaksi erilaista muotoilua. Jos kassavirta on tarkoitus saada alussa, niin se tunnetaan erääntyvän annuiteetin nykyarvona ja kaava voidaan johtaa kausimaksun, koron, vuosien lukumäärän ja vuodessa tapahtuvan esiintymistiheyden perusteella . Matemaattisesti se esitetään
PVA Due = P * (1 – (1 + r/n) -t*n ) * ((1 + r/n) / (r/n))
missä,
- PVA = elinkoron nykyarvo
- P = Määräaikainen maksu
- r = korko
- t = vuosien lukumäärä
- n = esiintymistiheys vuodessa
Jos kassavirta on tarkoitus saada kunkin kauden lopussa, niin se tunnetaan tavallisen annuiteetin nykyarvona ja kaava on hiukan erilainen ja se ilmaistaan
PVA Ordinary = P * (1 – (1 + r/n) -t*n ) / (r/n)
Esimerkkejä elinkorkokaavan nykyarvosta (Excel-mallilla)
Otetaan esimerkki ymmärtääksesi paremmin annuiteetin nykyarvon laskeminen.
Voit ladata tämän eläkevakuuden nykyarvon Formula Excel -mallin täältä - Eläkevakuuden nykyisen arvon Formula Excel -mallin nykyarvo.Elinkykykaavan nykyarvo - esimerkki 1
Otetaan esimerkki 5000 dollarin annuiteetista, jonka odotetaan saatavan vuosittain seuraavien kolmen vuoden aikana. Laske annuiteetin nykyarvo, jos diskonttokorko on 4%, kun maksu maksetaan kunkin vuoden alussa.
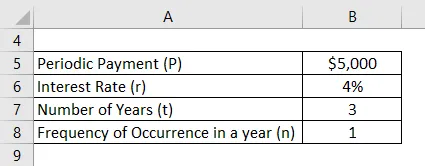
Ratkaisu:
Erääntyvien eläkkeiden nykyarvo lasketaan alla olevan kaavan avulla
PVA Erääntyy = P * (1 - (1 + r / n) -t * n ) * ((1 + r / n) / (r / n))
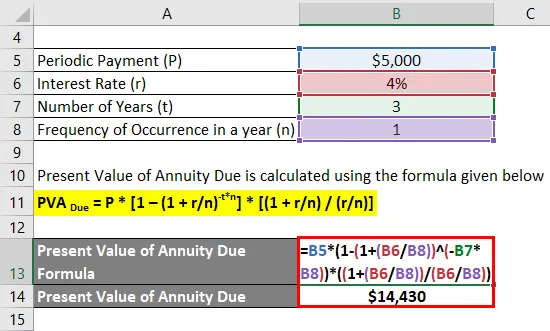
- Erääntyvien eläkkeiden nykyarvo = 5000 dollaria * (1 - (1 + (4% / 1)) -3 * 1 ) * ((1 + (4% / 1)) / (4% / 1))
- Erääntyvien eläkkeiden nykyarvo = 14 430 dollaria
Siksi annuiteetin nykyarvo on 14 430 dollaria.
Elinkykykaavan nykyarvo - esimerkki 2
Otetaanpa esimerkki Davidista, jonka odotetaan saavan saman verran tulevia neljännesvuosittaisia kassavirtoja 1000 dollaria seuraavien kuuden vuoden aikana. Laske tulevaisuuden kassavirran nykyarvo, jos voimassa olevaan markkinakorkoon perustuva diskonttokorko on 5% maksun vastaanottamisen aikana:
- Kunkin vuosineljänneksen alussa
- Kunkin vuosineljänneksen lopussa
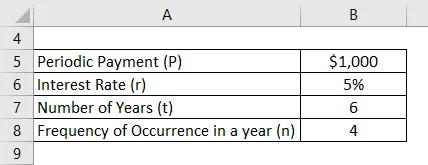
Ratkaisu:
Kunkin vuosineljänneksen alussa
Erääntyvien eläkkeiden nykyarvo lasketaan alla olevan kaavan avulla
PVA Erääntyy = P * (1 - (1 + r / n) -t * n ) * ((1 + r / n) / (r / n))
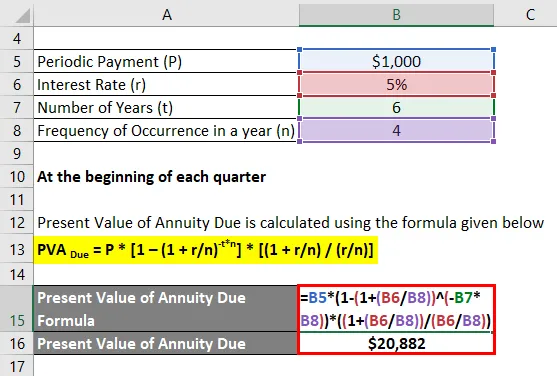
- Erääntyvien eläkkeiden nykyarvo = 1 000 * * (1 - (1 + (5% / 4)) -6 * 4 ) * ((1 + (5% / 4)) / (5% / 4))
- Erääntyvien eläkkeiden nykyarvo = 20 882 dollaria
Kunkin vuosineljänneksen lopussa
Tavallisen annuiteetin nykyarvo lasketaan alla olevan kaavan avulla
PVA tavallinen = P * (1 - (1 + r / n) -t * n ) / (r / n)
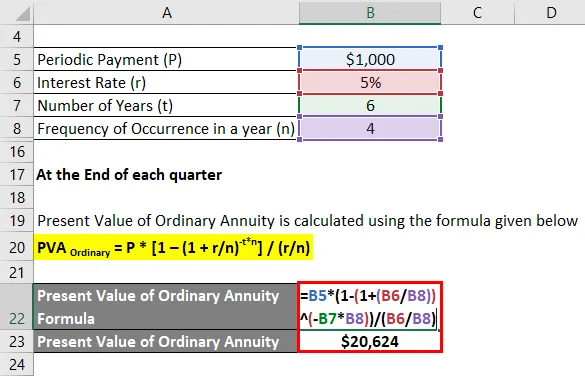
- Tavallisen annuiteetin nykyarvo = 1 000 dollaria * (1 - (1 + 5% / 4) -6 * 4 ) / (5% / 4)
- Tavallisen annuiteetin nykyarvo = 20 624 dollaria
Siksi Davidin vastaanottaman kassavirran nykyarvo on 20 882 dollaria ja 20 624 dollaria, jos maksut vastaanotetaan kunkin vuosineljänneksen alussa tai lopussa.
Selitys
Tarkastellaan ensin kaavaa maksettavan annuiteetin nykyarvolle ja sitten kaavaa tavallisen annuiteetin nykyarvolle ja jokainen niistä voidaan johtaa seuraavien vaiheiden avulla:
Vaihe 1: Ensin selvitetään sama määräaikainen maksu, jonka odotetaan suoritettavan joko kunkin kauden alussa tai lopussa. Sitä merkitään P.
Vaihe 2: Seuraavaksi selvitä korko voimassa olevien markkinakorkojen perusteella ja sitä käytetään diskonttaamaan jokainen määräaikainen maksu nykypäivään. Sitä merkitään r.
Vaihe 3: Seuraavaksi selvitä, kuinka monta vuotta tulevat maksut odotetaan vastaanottavan, ja sitä merkitään t: llä.
Vaihe 4: Määritä seuraavaksi maksujen tiheys tai esiintyminen vuodessa, ja sitä merkitään n. Sitä voidaan käyttää laskettaessa efektiivinen korko ja kausien lukumäärä alla esitetyllä tavalla.
Efektiivinen korko = r / n
Jaksojen lukumäärä = t * n
Vaihe 5: Jos kassavirta on tarkoitus saada kunkin kauden alussa, erääntyvän annuiteetin nykyarvon kaava voidaan johtaa määräaikaisen maksun (vaihe 1), efektiivisen koron (vaihe 4) ja jaksojen lukumäärä (vaihe 4), kuten alla on esitetty.
PVA Erääntyvä = P * (1 - (1 + r / n) -t * n ) * (1 + r / n) / (r / n)
Toisaalta, jos kassavirta on tarkoitus saada kunkin kauden lopussa, niin tavallisen annuiteetin nykyarvon kaava voidaan ilmaista alla esitetyllä tavalla.
PVA tavallinen = P * (1 - (1 + r / n) -t * n ) / (r / n)
Eläkevakuuden nykyarvon relevanssi ja käyttö
Vaikka annuiteetin nykyarvon käsite on yksinkertaisesti toinen ilmaus rahan aika-arvoteoriasta, se on tärkeä käsite eläkesuunnittelun arvioinnin kannalta. Itse asiassa sitä käyttävät pääasiassa kirjanpitäjät, vakuutusmatemaatikot ja vakuutushenkilöstö laskeakseen jäsenneltyjen tulevien kassavirtojen nykyarvoa. Se on hyödyllinen myös päätöksessä - onko kiinteämääräinen maksu parempi kuin diskonttokorkoon perustuvien tulevien maksujen sarja. Edellä mainittuun päätökseen vaikuttaa myös se, että maksetaanko maksu kunkin ajanjakson alussa vai lopussa.
Annuiteettikaavan laskurin nykyarvo
Voit käyttää seuraavaa elinkoronlaskurin nykyarvoa
| P | |
| R | |
| T | |
| n | |
| PVA | |
| PVA = | P x (1 - (1 + r / n) -txn ) X (1 + r / n / r / n) |
| = | 0 x (1 - (1 + 0/0 ) -0x0 ) X (1 +0 / 0/0/0 ) = 0 |
Suositellut artikkelit
Tämä on opas eläkevakuuden nykyarvoon. Tässä keskustellaan siitä, kuinka eläkeannin nykyarvo voidaan laskea käytännön esimerkkien avulla. Tarjoamme myös eläkkeiden nykyarvon laskurin ladattavalla excel-mallilla. Voit myös katsoa seuraavia artikkeleita saadaksesi lisätietoja -
- Kaava erääntyvien eläkkeiden tulevaisuuden arvolle
- Rahan aika-arvo laskurilla
- Kuinka laskea annuiteetti kaavan avulla?
- Alennuskerroinkaava (esimerkkejä Excel-mallilla)